［２］ＢＣＣ結晶

　　（３，４｝（１１０）

　　（３，３，４｝（０１００）

　　（３，３，３，４｝（０１１００）

　　（３，３，３，３，４｝（００１０００）

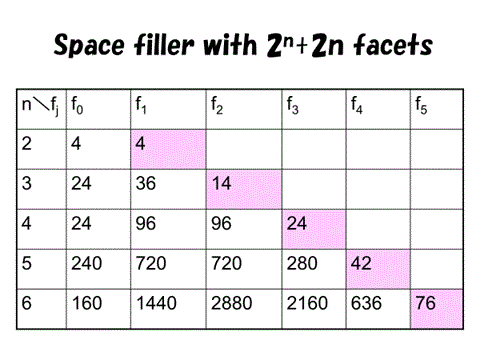
　すなわち，正軸体．立方体系の切頂多面体である．そのファセット数は２^n＋２ｎになるが，３次元では切頂八面体となり［１］と一致，４次元では２４胞体（正２４胞体），５次元では４２胞体となる．ただし，２次元では８角形ではなく４角形となる．３次元ではこれらと同じｆベクトルをもつ異なる多胞体はあるが，４〜６次元では存在しない．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

BCC結晶だけが面数を一般式で表すことができない。

[1]補正項が必要になること

[2]奇数次元と偶数次元で漸化式の形が異なること

が原因と思われる

fk formula

fk(n)= pk(n)+ qk(n)

k-face number of n-polytope

principal term (direct product)

pk(n)= Σtp+1kgj(n)fk-j(n-1-j) (k=tp+1_n-1)

correction term (inclusion-exclusion)

qk(n)= Σ0tp(-1) jgj(n)fk(n-1-j) (k=0_n-1)

gj(n)=2^(j+1)(n,j+1)

nが偶数のとき、tp=[n/2]-1

nが奇数のとき、tp=[(n-1)/2]-1

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

qk(n)= Σ0tp(-1) jgj(n)fk(n-1-j)

nが偶数のとき、fk(n-1-j)には2次元低いものは利用できない

nが奇数のときも、fk(n-1-j)には2次元低いものは利用できない

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

pk(n)= Σtp+1kgj(n)fk-j(n-1-j) (k=tp+1_n-1)

nが偶数のとき、fk(n-1-j)には(1,0,0,・・・)(0,1,0,・・・)(0,0,1,・・・)を利用できる

nが偶数のとき、fk(n-1-j)には正軸体のものと(1,0,0,・・・)(0,1,0,・・・)(0,0,1,・・・)を利用できる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

立方体側からやっても2次元低いものを利用できないこともわかった。

結局、一般式はうまくいかないことがわかった。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝