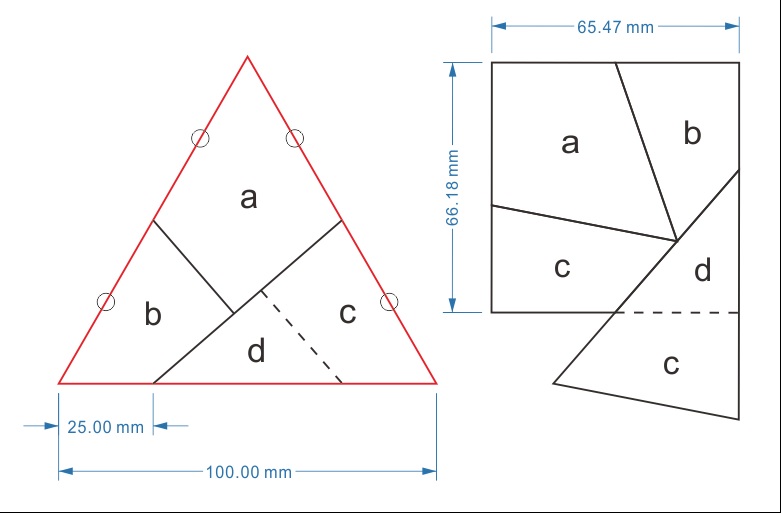
デュドニーは正三角形を4片に分解してそれを組み替えなおして正方形をつくるパズルを創作した。

パズル作家デュドニーが１９０２年に見つけたとされる．正三角形を正方形に（正方形を正三角形に）する４片裏返しなしの有名なパズルであり，ヒンジで４片を回転させて正三角形と正方形を相互変換させる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

デュドニーは正三角形を4片に分解してそれを組み替えなおして正方形をつくるパズルを創作したのであるが、ここでの問題は最小個数の部品の分割することである。デュドニー自身の答えは４片というものであった。　４片でないもの，裏返しのあるものは見つかっているが，４片かつ裏返しなしの解はこれ以外には見つかっていないという．

3片では不可能であるという証明も見つかっていなかったのであるが、上原隆平先生らが発表しました。 https://news.yahoo.co.jp/articles/69fc6af2f62350078ee7f4cd2737fce17a8b6a55?fbclid=IwZXh0bgNhZW0CMTAAAR1ZfrULwaha4FnkeENy6jD9Zn7j-4EfhkaCi9hPXXzvw2Om1z7PvIHTxD4_aem_kcMzSgh6L4oRdaK5ZNaz4Q

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

なお、中川宏さんが近似的な解体再編法の図を送ってくれたので、掲載する。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝