【１】準正多面体の対蹠点への最短パス

準正多面体のある頂点から辺を通ってその対蹠点まで到達することを考える。その最短パスを求めるのに辺を3色に着色して考える。

{3,4}(1,1,1)では9ステップで対蹠点に到達するが、これは正八面体群(B3)の対称面の数に一致する。

赤→緑→青→赤→緑→青→赤→緑→青の順にパスを選べば必ず対蹠点に到達することができるのである。

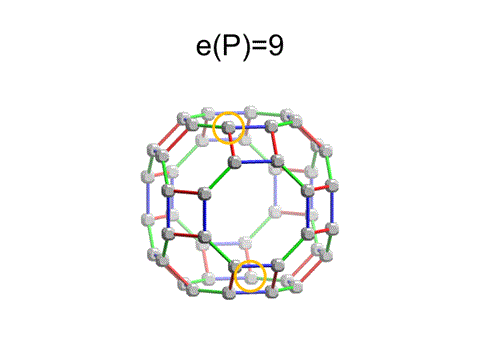
{3,4}(1,1,0)では青色の辺が退化したものと考えられる。したがって、最短パスは9の1/3-2/3の間になると推察されるが、実際、最短パスは6である。

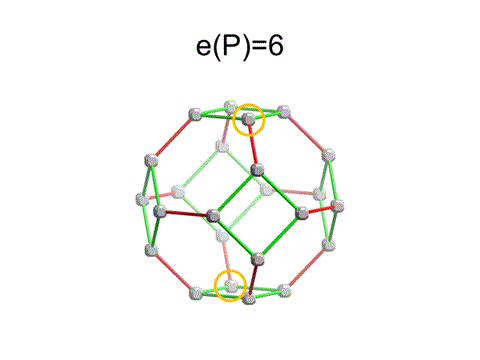
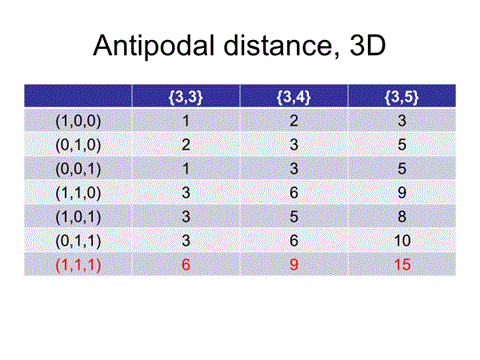
3次元では表のうえ3個が原始的多面体(111)の最短パスの1/3以下、中３個が原始的多面体(111)の最短パスの1/3-2/3以下になることを容易に確かめることができる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】高次元準正多面体の対蹠点への最短パス

このことは高次元でも成り立っている。たとえば、6次元の場合、その最短パスを求めるのに辺を6色に着色して考えることができる。

{3,3,3,3,4}(1,1,1,1,1,1)では36ステップで対蹠点に到達するが、これはB6群の対称面の数に一致する。

赤→黄→緑→茶→黒→紫→赤→黄→緑→茶→黒→紫→・・・の順にパスを選べば必ず対蹠点に到達することができるのである。

{3,3,3,3,4}(0,1,0,1,1,0)では赤・緑・紫が退化したものと考えられる。したがって、最短パスは9の2/3-1/2の間(12,18]になると推察されるが、実際、最短パスは16である。

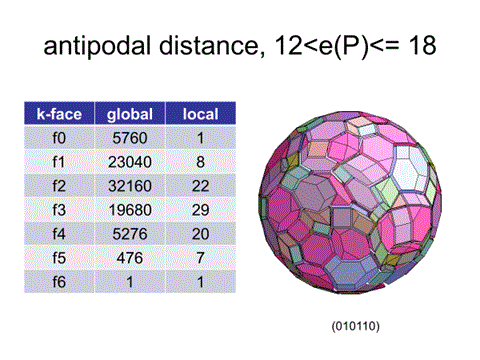
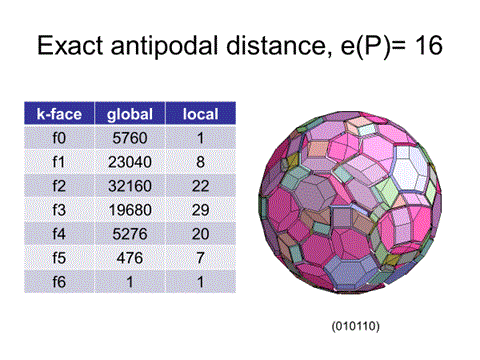
6個のパラメータで63個の準正多面体の対蹠点への最短パスを求めようとしているのであるが、コンピュータなしに正確な最短パスを求めるとなると、どうすればよいのだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝