【１】身の回りの数学を探す

2次元では6角形が安定な平面充填

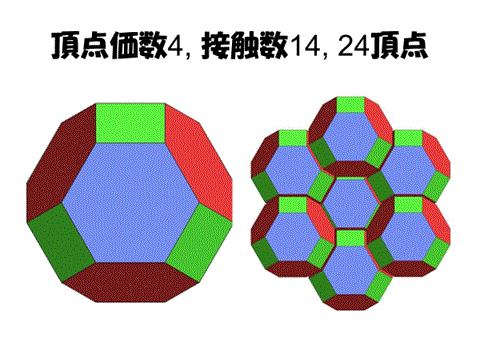
3次元では14面体が安定な空間充填となっている。

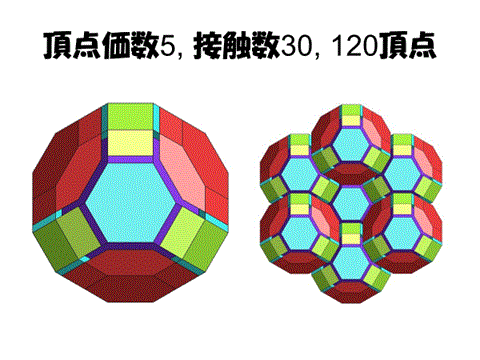
それでは4次元では周囲のいくつの細胞に接触した状態で、安定な空間充填となるのだろうか？

答えを先に言うと、30胞体なのであるが、直観的にそれを求めるアイデアがある。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

3層構造になっていると考える。

2次元ではおなじ層に2つ、上の層に２つ、下の層に2つで計６個になっている

3次元ではおなじ層に6つ、上の層に4つ、下の層に4つで計14個になっている

4次元ではおなじ層に14、上の層に8、下の層に8で計30個になる

n次元では同じ層にFn-1,上の層に2^(n-1)、下の層に2^(n-)で計Fn個になると考えると

Fn=Fn-1+2・2^(n-1)=Fn-1+2^n

Fn=2(2^2-1)が得られる。

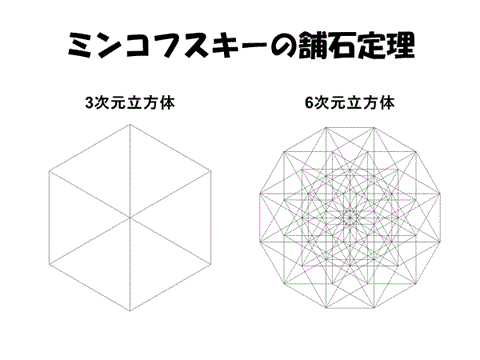
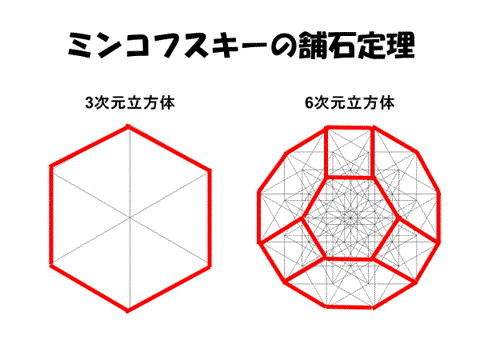
この形はn(n+1)/2次元立方体のn次元空間への射影として得られるのであるが、積み重ねるとA群空間充填と呼ばれる安定した構造をとることになる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝