【１】身の回りの数学を探す

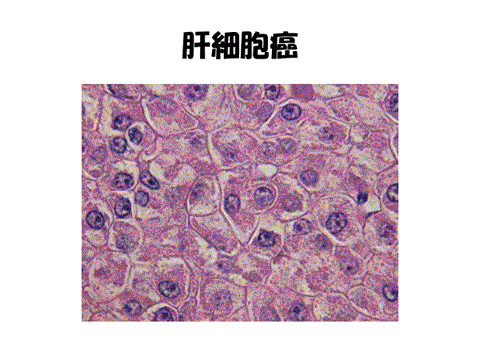
私の本職は病理医である。顕微鏡をして診断したり、遺伝子解析して癌ごとに最適な抗がん剤を決定するというのが役目である。日常業務のなかから数学を探すと、この癌細胞は何面体?,すなわち、周囲の細胞何個と接触しているのかという素朴な疑問がわく。プレパラートで見えているのは厚さ3ミクロンの世界であるから、いくら顕微鏡を覗いたところで、答えは得られない。

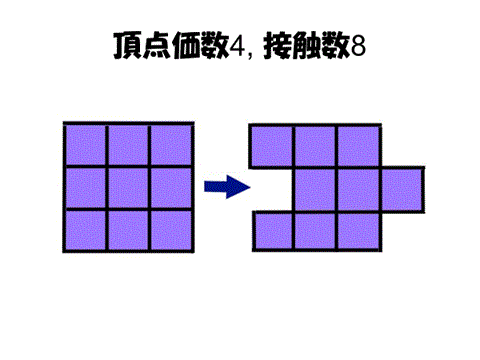
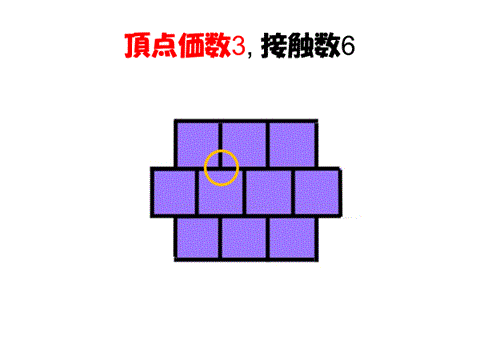
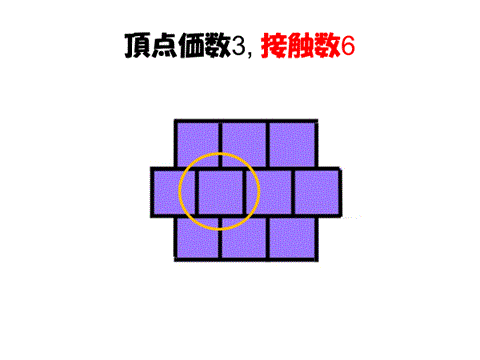
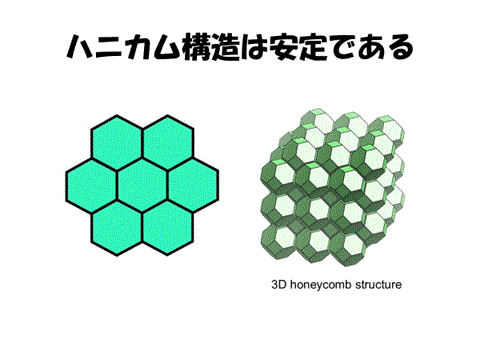
そこで次元を１次元下げて考えることになる。2次元では頂点次数3(一つの頂点の周りに3個の細胞が配置)、接触数6(一つの細胞の周りに6個の細胞が配置)した状態が安定であると考えられる。3次元では3層構造を考えると、同じ層で6個の細胞が接触、上の層で4個、下の層で4個の細胞が接触するのが安定で、頂点次数4、接触数14となる。

すなわち、この癌細胞は14面体で、これは観察から得られたデータ：13-14面体に一致することがわかる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この講演を聞いた生徒の感想。

形は無意味にそこに存在するものではなく、理由があってその形として存在していることがわかりました。普段あまり考えない形がその形である理由に着目することで、その形が形全体の安定に貢献していたり、そこから美しさを感じたりすることができる、そのような形の可能性に気付かされました。また、ハニカム構造などそれを自然が創り出していることに驚きました。・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝