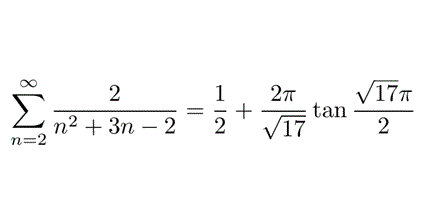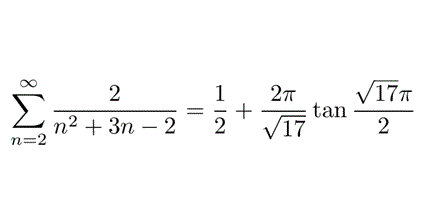以下のような問題が理科大で出ました。収束しますし、調和数列の和とは違いますが、バーゼル問題の親戚です。しかし、高校数学の範囲外です。(T)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

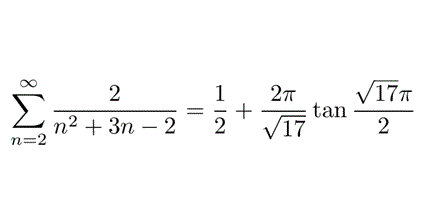
tanxのテイラー展開から

π/x・tan(πx/2)=Σ(1,∞)1/{k^2-k+(1-x^2)/4}

π/√17・tan(π√17/2)=Σ(1,∞)1/{k^2-k-4}

にたどり着くのさえ難しい。

|x|＜π/2

tanx=x+x^3/3+2x^5/15+17x^7/315+62x^9/2835+1382x^11/155925+・・・

1/x・tanx=1+x^2/3+2x^4/15+17x^6/315+62x^8/2835+1382x^10/155925+・・・

2/πx・tan(πx/2)=1+(πx/2)^2/3+2(πx/2)^4/15+17(πx/2)^6/315+62(πx/2)^8/2835+1382(πx/2)^10/155925+・・・

2π/x・tan(πx/2)=π^2{1+(πx/2)^2/3+2(πx/2)^4/15+17(πx/2)^6/315+62(πx/2)^8/2835+1382(πx/2)^10/155925+・・・}

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

無限乗積を用いると

Π(1-x^2/(2n)^2)=2sin(πx/2)/πx

Π(1-x^2/(2n-1)^2)=cos(πx/2)

2/πx・tan(πx/2)=Π(1-x^2/(2n)^2)/(1-x^2/(2n-1)^2)

これを無限級数の形にするには・・・？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Σ(0,∞)x^2n/(2n)!=cosx

Σ(0,∞)x^2n/(2n+1)!=sinx/x

これからどうやって

π/x・tan(πx/2)=Σ(1,∞)1/{k^2-k+(1-x^2)/4}

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝