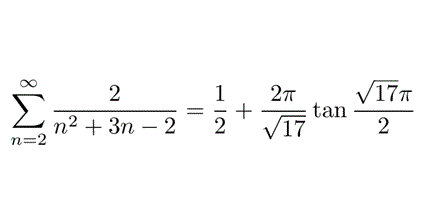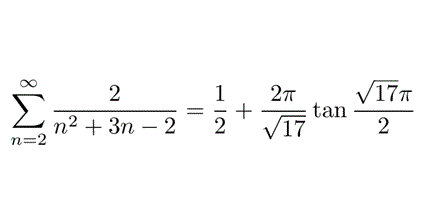以下のような問題が理科大で出ました。収束しますし、調和数列の和とは違いますが、バーゼル問題の親戚です。しかし、高校数学の範囲外です。(T)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

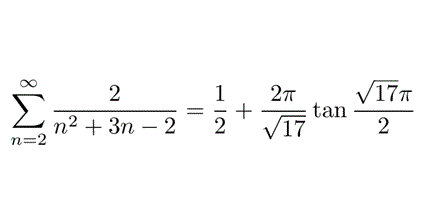
最初に考えた解法は

p=(3-√17)/2＞-1

q=(3+√17)/2＞-1として

Σ(1,∞)1/(n^2+3n-2)=Σ(1,∞)1/(n+p)(n+q)

=1/(q-p)・{(1/(p+1)-1/(q+1))+(1/(p+2)-1/(q-2))+・・・}

=1/(q-p)・∫(0,1)(x^p-x^q)・(1+x+x^2+・・・)dx

=1/(q-p)・∫(0,1)(x^p-x^q)/(1-x)dx

しかし、この積分がわからない・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

仕方がないので、公式集を眺めていると

tan(πx/2)=4x/π・Σ(1,∞)1/{(2k-1)^2-x^2}

π/x・tan(πx/2)=Σ(1,∞)4/{(2k-1)^2-x^2}

π/x・tan(πx/2)=Σ(1,∞)1/{k^2-k+(1-x^2)/4}

π/x・tan(πx/2)=4/(1-x^2)+Σ(2,∞)1/{k^2-k+(1-x^2)/4}

x=√17を代入すると

π/√17・tan(π√17/2)=-1/4+Σ(2,∞)1/{k^2-k-4}

正解にはたどり着かない・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Σ(2,∞)1/{n^2+3n-2}=1/8+1/16+1/26+1/38+・・・

Σ(2,∞)1/{k^2-k-4}=-1/2+1/2+1/8+1/16+1/26+1/38+・・・=1/8+1/16+1/26+1/38+・・・=Σ(2,∞)1/{n^2+3n-2}

やれやれ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Σ(4,∞)1/{k^2-k-4}=Σ(2,∞)1/{(k+2)^2-(k+2)-4}=Σ(2,∞)1/{k^2+3k-2}

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

小細工が何重にも張り巡らされている印象であるが、小細工なしに

π/x・tan(πx/2)=Σ(1,∞)1/{k^2-k+(1-x^2)/4}

π/√17・tan(π√17/2)=Σ(1,∞)1/{k^2-k-4}

と表してみたいところである。

π/√5・tan(π√5/2)=Σ(1,∞)1/{k^2-k-1}

π/3・tan(π3/2)=Σ(1,∞)1/{k^2-k-2}・・・発散

π/√13・tan(π√13/2)=Σ(1,∞)1/{k^2-k-3}

π/√17・tan(π√17/2)=Σ(1,∞)1/{k^2-k-4}

π/√21・tan(π√21/2)=Σ(1,∞)1/{k^2-k-5}

π/5・tan(π5/2)=Σ(1,∞)1/{k^2-k-6}・・・発散

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

π/x・tanh(πx/2)=Σ(1,∞)1/{k^2-k+(1+x^2)/4}

π/√3・tanh(π√3/2)=Σ(1,∞)1/{k^2-k+1}

π/√7・tanh(π√7/2)=Σ(1,∞)1/{k^2-k+2}

π/√11・tanh(π√11/2)=Σ(1,∞)1/{k^2-k+3}

π/√15・tanh(π√15/2)=Σ(1,∞)1/{k^2-k+4}

π/√19・tanh(π√19/2)=Σ(1,∞)1/{k^2-k+5}

π/√23・tanh(π√23/2)=Σ(1,∞)1/{k^2-k+6}

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝