Mathematica関連書籍

　　ワゴン「Mathematicaによる現代数学探究」基礎編，ｐ２２

に載っている記事で，

　　Sin[x]+ArcSin[x] = 2x

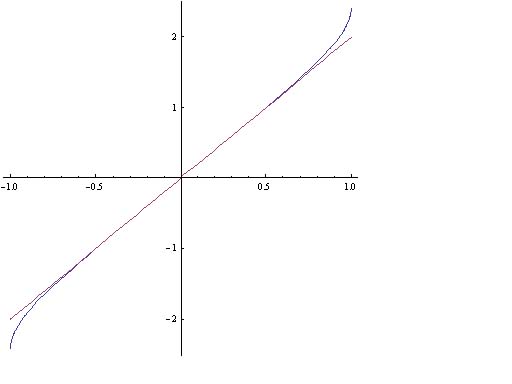
というのがある．この式はむろん正しくないのだが，−０．８から０．８までプロットすると本当に直線のように見える（−１から１までプロットすれば直線でないことはわかるのだが・・・）．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　Sin[x]+ArcSin[x]の０周りのテイラー級数（マクローリン級数）を調べると

　　2x+x^5/12+2x^7/45+5513x^9/181440+2537x^11/113400+4156001x^13/239500800+･･･

すなわち，３次の項が偶然の相殺され，関数が直線に近いものになっていることが判明した．５次以降の項は係数が小さいことから［−０．８，０．８］の区間では非常に小さいものとなる．グラフを描画しているときに，たまたま上記の式が成り立つようなグラフが得られたそうだ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ここで、F(x)=2x-sinx-arcsinxを考える。

x=11を代入すると、

F(11)=22-sin11-arcsin11

sin11〜-1

π〜22/7より、11〜7/2・πであるから

sin11〜-1

だが、arcsin11はNGである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝