＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正多面体（正四面体・正八面体・正20面体）の稜の数は

6=2・3、12=3・4、30=5・6

という性質を満たす。

また、基本領域数は

2(1+3+3+5)=24

2(1+5+7+11)=48

2(1+11+19+29)=120

個の単体錐に分割される。

各項は素数であるが、各項に１を足すと

(2,4,4,6)

(2,6,8,12)

(2,12,20,30)

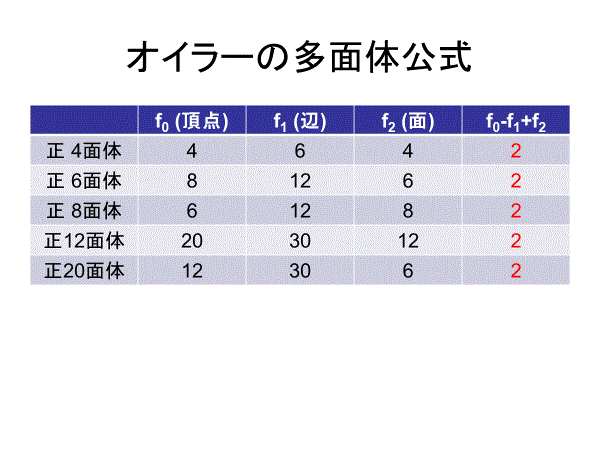
すなわち、頂点数、面数、稜数になっている

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正四面体・正八面体・正20面体の固有方程式を解くと、それぞれ

m=(1,2,3)

m=(1,3,5)

m=(1,5,9)

Σm=6

Σm=9

Σm=15

Π(m+1)=24

Π(m+1)=48

Π(m+1)=120

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝