種村正美先生（統計数理研）は平面・球面・空間における最適配置の逐次生成についてご講演された。

いずれの場合にも重心法が最も優れているという結果であった。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

特に興味深かったのは、球面最適配置で、

v12では5^12

v14では5^126^2（ゴールドバーグの14面体）が生成されるというものであった。

ケルビンの14面体4^66^8は実現されず、逆に、ウィア・フェラン構造5^12+5^126^2が実現される根拠となるものだろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

なお、一般に

　　４ｆ2＋３ｆ3＋２ｆ4＋ｆ5−ｆ7−２ｆ8−３ｆ9−・・・＝１２

が成り立つ。

五角形面と六角形面よりなる多面体では

f5=12

すなわち、五角形面数は常に12となる。

それが14面体であれば5^126^2（ゴールドバーグの14面体）なのである。

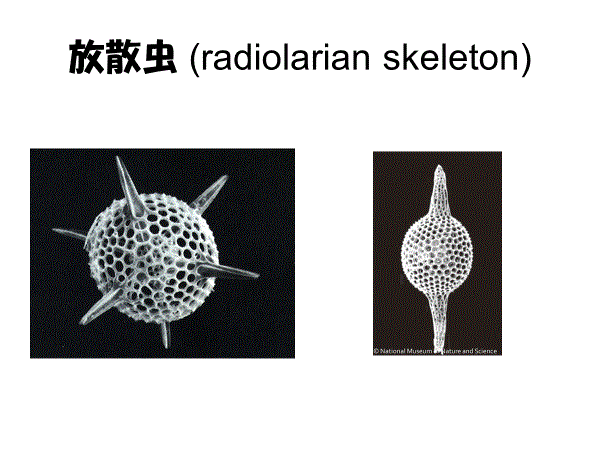
また、放散虫の骨格はf5,f6,f7からなるが

f5=12+f7

が成り立つ。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝