仭傾儕僗僞僀僆僗偺徹柧乮偦偺侾侾乯
婭尦慜320擭丄傾儕僗僞僀僆僗偼乽俆偮偺惓懡柺懱偺斾妑乿偲偄偆杮傪弌偟丄偦偺拞偱
乽惓12柺懱偲惓20柺懱偑摨堦偺媴偵撪愙偡傞偲偒丄惓12柺懱偺俆妏宍偲惓20柺懱偺俁妏宍偼摨偠墌偵撪愙偡傞乿
偙偲傪徹柧偟偨丅寁嶼偟偰妋偐傔偰傒偨偄丅
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
倓傪媴偺捈宎丄倱傪撪愙偡傞惓懡柺懱偺曈偺挿偝偲偡傞偲
(a)惓巐柺懱丗d^2=3/2丒s^2
(b)惓敧柺懱丗d^2=2丒s^2
(c)棫曽懱丗d^2=3丒s^2
(d)惓20柺懱丗d^2=(5+併5)/2丒s^2
(e)惓12柺懱丗d^2=3(3+併5)/2丒s^2
夵傔偰寁嶼偟側偍偟偰傒傞偲
(d)惓20柺懱偱偼墶暆^2=4冇^2,s^2=3
d^2=4冇^2+乮冇^2-2)^2=4冇^2+1/冇^2=4冇+4-冇+2=3冇+6亖3併5冇
d^2/s^2=併5冇亖(5+併5)/2偑惉傝棫偮
(e)惓12柺懱偱偼墶暆^2=4冇^2,s^2=併5/冇
d^2=4冇^2+乮冇^2-2)^2=4冇^2+1/冇^2=4冇+4-冇+2=3冇+6亖3併5冇
d^2/s^2=3冇^2亖3(3+併5)/2偑惉傝棫偮
扨埵墌偵撪愙偡傞5妏宍偲3妏宍偺曈偺挿偝偼偦傟偧傟
s12=2sin36亖{(10-2併5)^1/2}/2
s20=2sin60=併3
(5+併5)/2丒3=3(3+併5)/2丒{(10-2併5)}/4偼惉傝棫偮偩傠偆偐丠
(5+併5)=(3+併5)丒{(10-2併5)}/4丒丒丒OK
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖
柾宆偼擄偟偄偺偱丄GIF摦夋偵偟偰傒傑偟偨丅丂丂乮嶳丂寷媣乯
懡柺懱栘岺偼堦斒偵棫曽懱偐傜傎偐偺惓懡柺懱傪嶍傝弌偟傑偡偑丄偙偺応崌偼丄媴懱偐傜堦條偵彫墌抐柺傪愗傝棧偡憖嶌偵傛偭偰丄偡傋偰偺惓懡柺懱傪嶍傝弌偡偲憐掕偟傑偡丅摨偠戝偒偝偺媴懱偐傜嶍傝弌偟偨惓榋柺懱偲惓敧柺懱丄偦偟偰惓廫擇柺懱偲惓擇廫柺懱偲偑丄偦傟偧傟摿掕偺曽岦偐傜尒傞偲摨偠戝偒偝偺彫墌抐柺偐傜側傞偙偲偑傢偐傝傑偡丅
[1]媴偵撪愙偡傞惓20柺懱
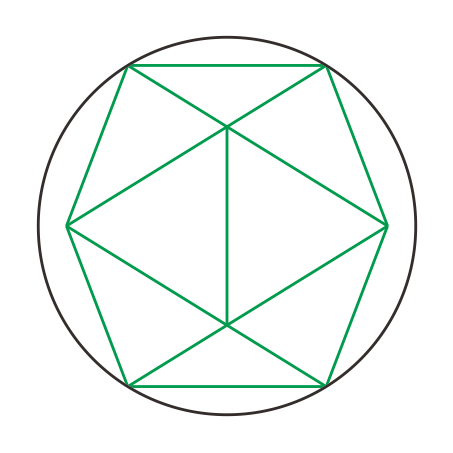
[2]媴偵撪愙偡傞惓12柺懱
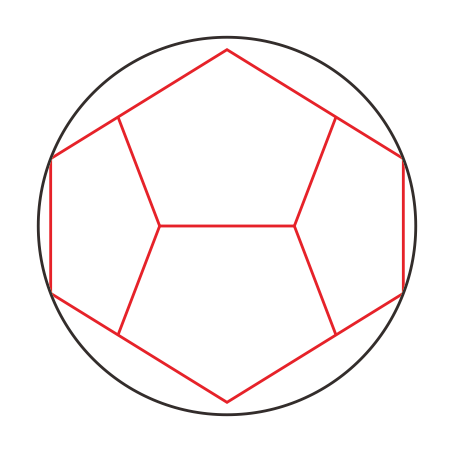
[3]摨偠墌偵撪愙偡傞
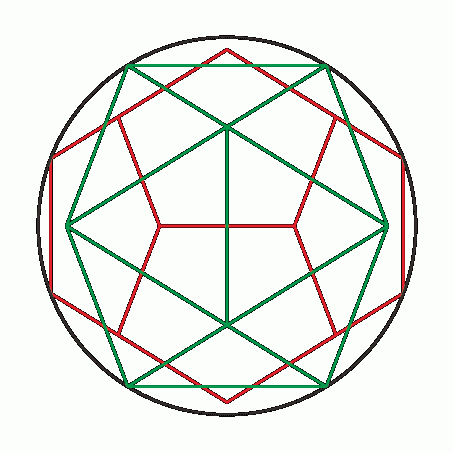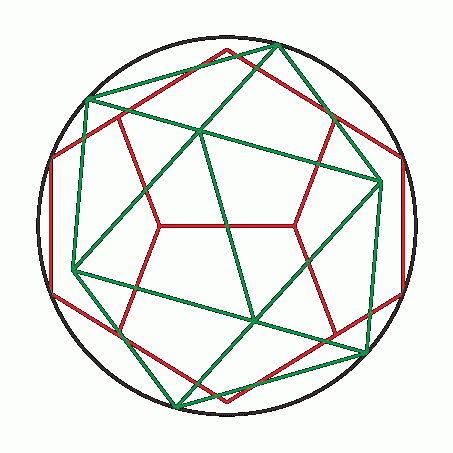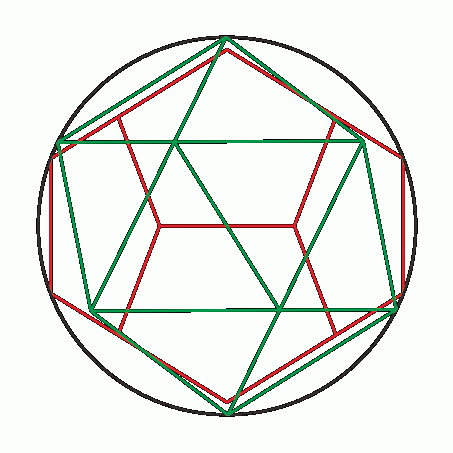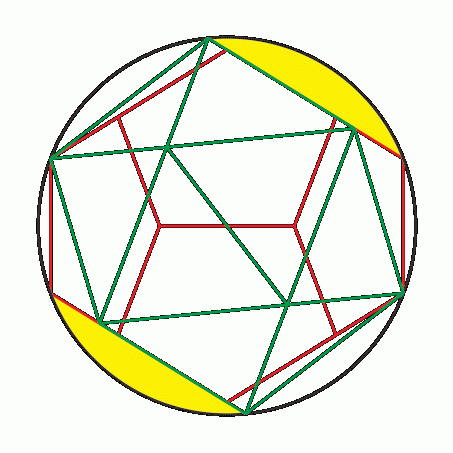
惓20柺懱偲惓12柺懱偑摨偠媴偵撪愙偡傞偲偒丄拞恎偺媗傑偭偨媴懱偐傜彫墌抐柺傪愗傝棊偲偡偲峫偊傞偲丄俀偮偺棫懱偺奺柺傪娷傓彫墌抐柺偼媴偺拞怱偐傜摨偠嫍棧偵側傞
憃懳偼捠忢捀揰偲柺怱傪岎姺偡傞憖嶌偲巚傢傟偰偄傑偡偑丄偦偺嵺偵偼奜愙媴偺戝偒偝偑曄傢偭偰偟傑偄傑偡丅偲偙傠偑奜愙媴偺戝偒偝傪屌掕偡傞偲丄摨偠戝偒偝偺彫墌抐柺傪愗傝庢傞幉偺堘偄乮惓榋柺懱丗俁杮偲惓敧柺懱丗係杮丄惓廫擇柺懱丗俇杮偲惓擇廫柺懱丗侾侽杮乯偲偟偰憃懳偑偲傜偊傜傟傞偲巚偄傑偡丅乮惓巐柺懱偺応崌偼惓敧柺懱偺応崌偲摨偠係杮偺幉偺惓曽岦偲晧曽岦偱憃懳偲側傝傑偡丅乯
亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖亖





