紀元前320年、アリスタイオスは「５つの正多面体の比較」という本を出し、その中で

「正12面体と正20面体が同一の球に内接するとき、正12面体の５角形と正20面体の３角形は同じ円に内接する」

ことを証明した。

同じく双対の

「正8面体と正6面体が同一の球に内接するとき、正8面体の3角形と正6面体の4角形は同じ円に内接する」

は成り立つこともわかった。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

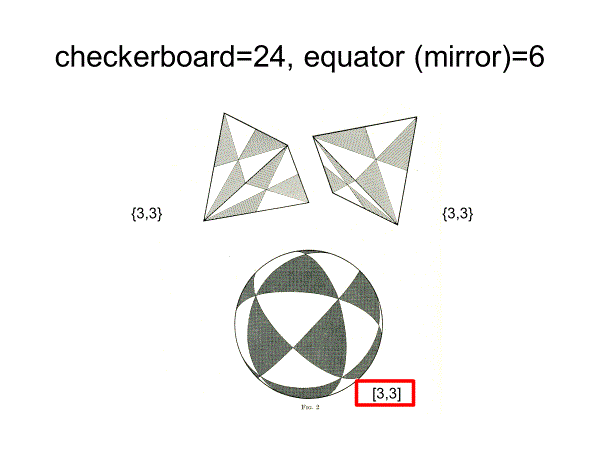
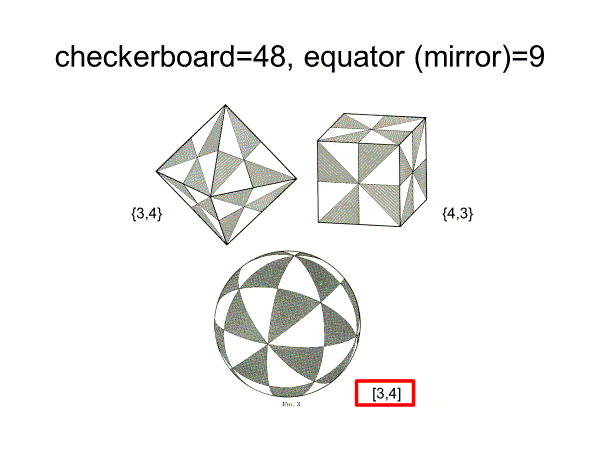
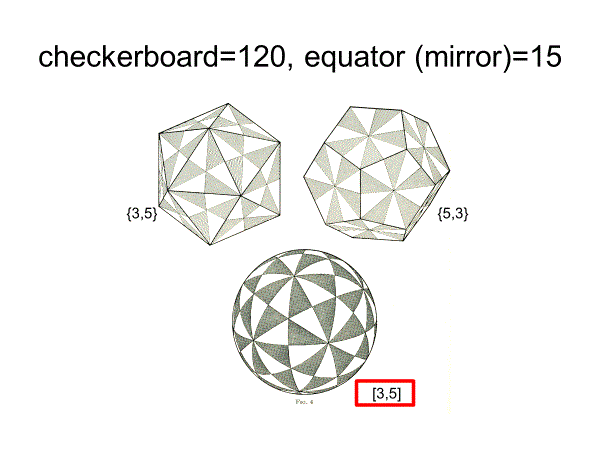
これらは、以下の図から直観的に証明可能である。外接円の半径は基本領域の一番長い線（直角三角形の斜辺）となるからである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝