正多角形は無限に多く存在しますが、それでは、「互いに合同な正多角形を隙間も重なりもないように並べて平面を完全に埋める仕方が何通りあるでしょうか？」この問題は昔から知られていて、それが３種類に限ることは以下のようにして証明されます。

　正多角形の中で平面をタイル張りのように隙間なく埋めつくすことができる平面充填形では、各頂点に正ｐ角形がｑ面が会するとすると、正ｐ角形の一つの内角は２（１−２／ｐ）×９０°であり、一つの頂点の回りの内角の和はこれがｑ個集まって四直角ですから、

　　２ｑ（１−２／ｐ）＝４、すなわち、

　　１／ｐ＋１／ｑ＝１／２　　　（ｐ，ｑ≧３）

で、この条件を満たす（ｐ，ｑ）の組は（３，６），（４，４），（６，３）の３通りしかありません。したがって、平面充填形は正三角形、正方形、正六角形の３つだけです。このうち正方形のは碁盤、正六角形のは蜂の巣などでおなじみでしょう。

　２次元の平面の中に正多角形は無限に多くあるのに反して、３次元の空間には無限に多くの正多面体は存在しません。平面充填形は、面数が無限大となって全体が一面に広がってしまった正多面体と解釈することができますが、平面充填形の場合と同様にして、正多面体の各面を正ｐ角形、各頂点にｑ面が会するとすると、頂点の周囲は４直角未満ですから、不等式

　　２ｑ（１−２／ｐ）＜４、すなわち、

　　１／ｐ＋１／ｑ＞１／２　　　（ｐ，ｑ≧３）

　　（ｐ−２）（ｑ−２）＜４

が正多角形となる必要条件です。このような整数の組は（ｐ，ｑ）＝（３，３），（３，４），（３，５），（４，３），（５，３）の５通りで、それぞれ、正４面体、正８面体、正２０面体、正６面体、正１２面体に対応します。

　すなわち、正多面体は正４・６・８・１２・２０面体の５種類あって５種類しかないことはプラトンの時代にはすでに見つけられていて、それらがプラトンの自然哲学で重要な役割を演ずるところから、正多面体はプラトンの立体（Platonic solid）とも呼ばれています。正多面体はピタゴラス学派には神秘的完全性の象徴のように見え、ギリシャの自然哲学者はこれらを５元素と対応させています。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

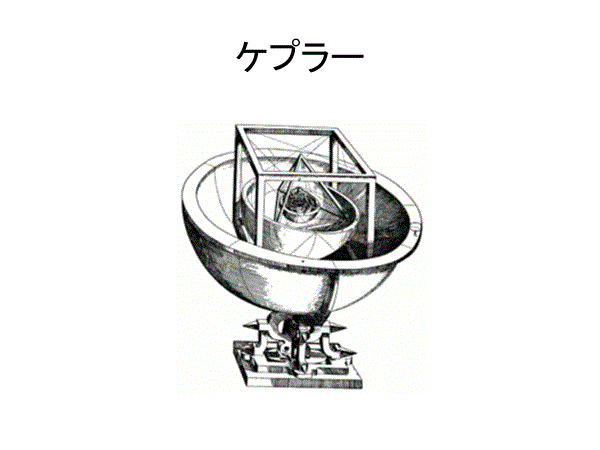
　ケプラーは惑星運動の法則を発見した天文学者として有名ですが、著名な数学者でもありました。事実、星形正多面体と呼ばれる凹型多面体の発見は彼の大きな業績です。ケプラーは「宇宙の神秘」（１５９６年）、「新天文学」（１６０９年）、「世界の調和」（１６１９年）という三部作を著していますが、非常にピタゴラスとプラトンびいきであって世界は数学的な調和、幾何学的秩序に従っていると確信し、彼の初期の著作「宇宙の神秘」では、太陽系の惑星の軌道を無数にある立体の中で明確な法則性をもっている立体（５種類の凸型正多面体）で幾何学的に説明しようとしていたことはよく知られています。

　当時、惑星は水金地火木土の６つしかないといわれていて、水星から土星までの間に５カ所の隙間ができますが、惑星の軌道は５種類の正多面体を次々同一の中心をもつ６個の球面に外接させて得られる、すなわち、この隙間に５つしかないプラトンの正多面体をすっぽりと入れ込むことができると主張しました。もちろん、ケプラーの法則を発見する以前の話で、天王星、海王星、冥王星の存在を知らなかったのです。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【おまけ】ただ意味もなく…

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝