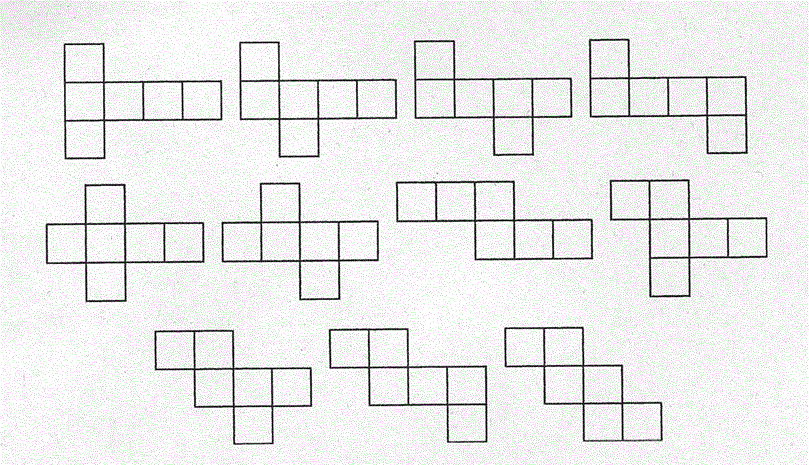立方体を展開して得られるラテンクロス（十字架形）はよく知られた形であるが，辺と辺を貼り合わせることにより，驚いたことに５種類の凸多面体は折れるという．ラテンクロスは５通りの多面体になる多角形というわけである．

　　［参］ドメイン＆オルーク「幾何的な折りアルゴリズム＜リンケージ，折り紙，多面体＞」上原隆平訳，近代科学社

によれば，それらは，２重に合わさった平坦な四角形（二面体），不等辺四面体，五面体，立方体，不等辺八面体である．

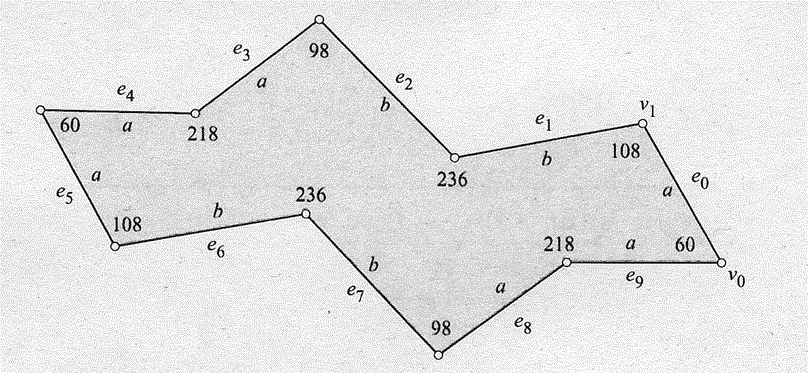
［１］５通りの多面体になる多角形

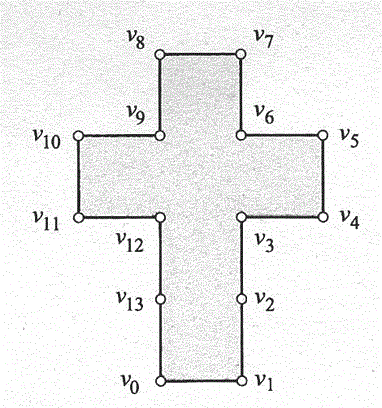
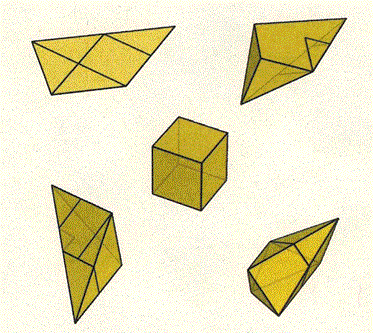
({e0,e3),{e1,e2},{e4,e13}.{e5,e6},{e7,e12},{e8,e11},{e9,e10})

({e0,e1),{e2,e3},{e4,e13}.{e5,e6},{e7,e12},{e8,e11},{e9,e10})

({e0,e3),{e1,e2},{e4,e9}.{e5,e8},{e6,e7},{e10,e13},{e11,e12})

({e0,e3),{e1,e2},{e4,e7}.{e5,e6},{e8,e9},{e10,e13},{e11,e12})

　さらに８５通りの折り方で互いに異なる２３種類もの多面体を折ることができると聞くと多くの人にとって大きな驚きなのではなかろうか．

［２］２３通りの多面体になる多角形

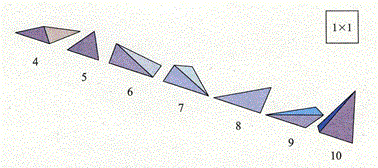
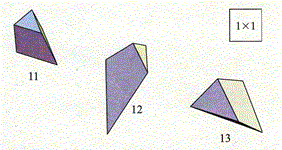
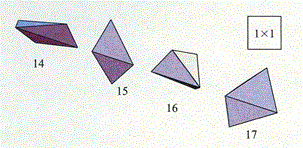
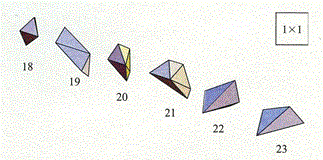
［３］２通りの多面体になる多角形

({e0,e3),{e1,e2},{e4,e9}.{e5,e8},{e6,e7})

({e0,e5),{e1,e2},{e3,e4}.{e6,e7},{e8,e9))

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】重なる展開図？

　正四面体を辺で切り開いた展開図は２通り，立方体と正八面体の展開図は１１通り，正１２面体と正２０面体では４３３８０種類もの展開図が存在することは古くから知られていた．

［４］立方体の１１通りの展開図

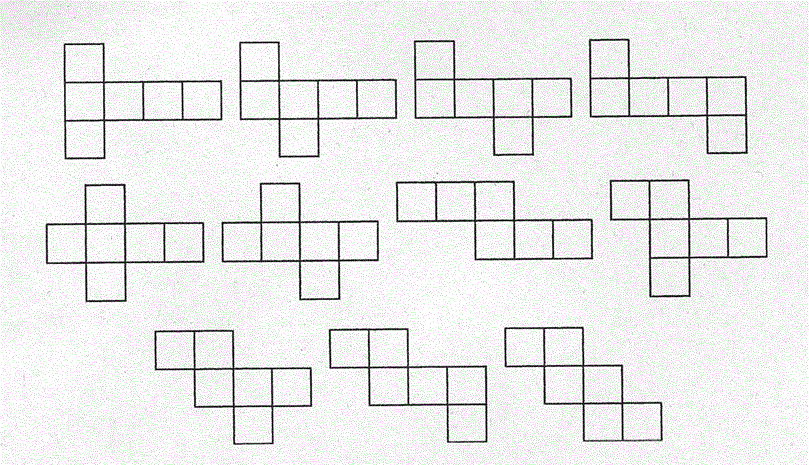
　しかし，この中には重なる展開図はひとつもないのである．これらすべてが重ならない展開図であることが証明されたのは２０１１年のことであるそうだ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】複数の箱が折れる展開図

　２通りのは個が折れる展開図は存在するだろうか．１９９９年，ビードルは２つの解を得た．

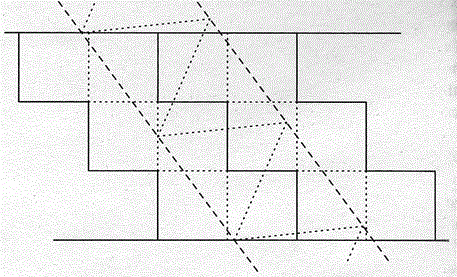
［５］２通りの直方体を折ることのできる多角形

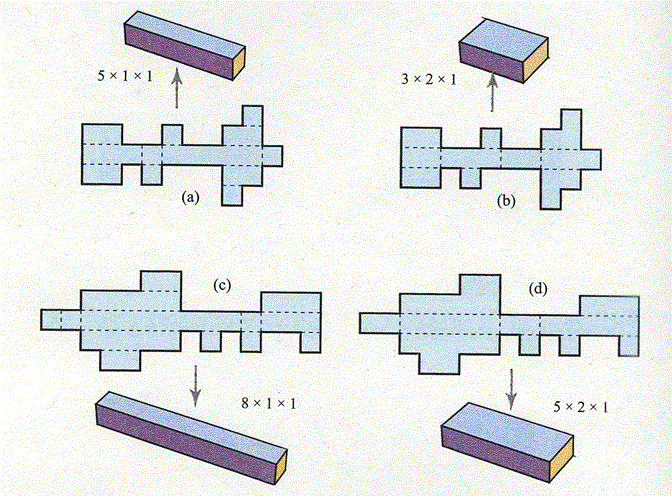
　２００８年，上原隆平先生（現ＭＩＴ）は２通りの箱が折れる展開図は無限に存在することを証明し，２０００個以上の解を発見した．２０１２年，（体積が０でない）異なる箱を３種類折れる展開図も無限個存在することが証明されている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】複数の多面体が折れる展開図

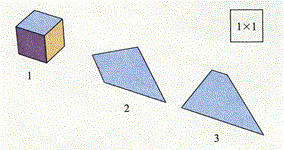
［６］正四面体と直方体を折ることのできる多角形

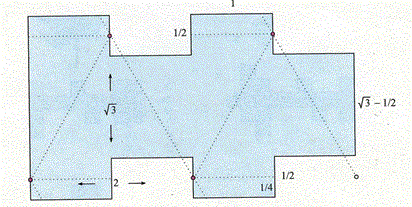
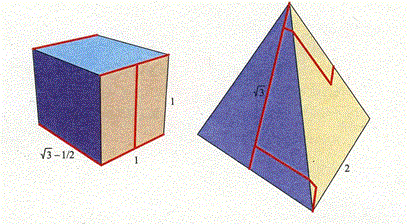
１辺の長さが２の正四面体と辺の長さが１×１×１．２３（＝√３−１／２）の直方体．

［７］正八面体と四面体を折ることのできる多角形

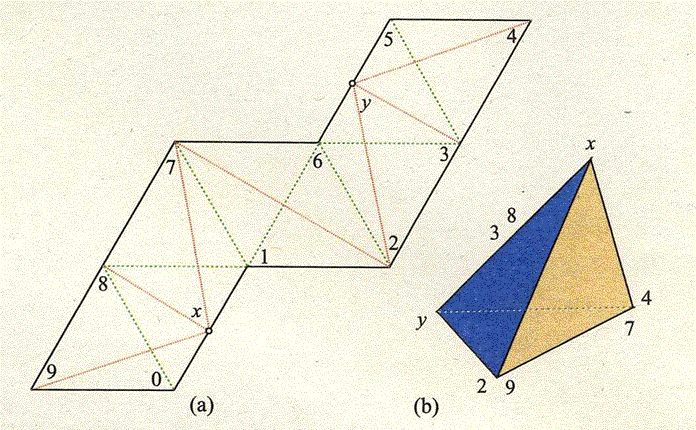
［８］立方体とほぼ正四面体を折ることのできる多角形

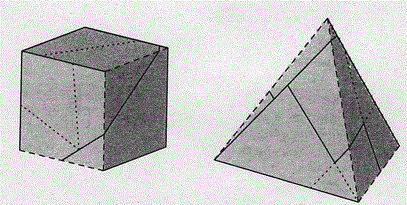
　ほぼ正四面体とはすべての面が合同な四面体で，辺の長さの誤差は高々２．８９×１０^-1796である（相当０に近い）．

　ある意味，立方体と正四面体を折ることのできる展開図が存在することは示されたが，正四面体以外の複数の正多面体を折れる共通の展開図は存在するだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝