僧侶・乙部融朗(1924-？)はわが国の高次元正多体胞模型研究の第一人者である．氏にとって４次元は見えるだけではなく，香り，聞こえるものであり，それを触れられる形にしたものが氏の４Ｄ模型である．

　４Ｄを３Ｄに投影すると内部構造をもった模型になるし，計量的な性質を保存するためには全体を少し歪める位相幾何学的変形も必要になってくる．このことについて，氏から「４Ｄにナジミの無い方にも解るように説明をつけたい」との有り難い申し入れがあり，本ＨＰに掲載の運びとなった．

　氏の記述は意味深で，私もそこに込められた氏の思いがはじめは理解できなかった．しかし，幾何学とは幼児が大好きなおもちゃで何時間も飽きることなく遊び続けるように，無邪気に４Ｄと遊ぶことが大切だということがおぼろげながら見えてきた．幾何学＝戯画学の本質とはアタマだけでなく，目耳鼻手を働かせて真剣に遊ぶことが研究なのであると・・・．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［１］「４次元が必要な分野」

　４次元以上の数学で扱わなければならない物理現象は沢山ありますが，これを高次元空間の現象として便利していますが，３次元以上の空間そのものが実在するのダということは人間の理解を越えています．アインシュタインによって距離は光の到達する時間であると喝破されたので，総ての物理現象は時間の変化の関数であるので，４次元時空としての尺度を用いますが．

［２］「脳産物としての４次元図形」

　４０年以上４次元準正多体胞の全貌を尽きとめるべく過ごして来た私もようやく，純空間はあくまで３次元であるとの覚悟に到りましたが，４次元図形というものは数学的脳産物として十分に考え得るものです．ある意味で思考の勝利でもありますが困迷でもあります．諸兄をこのドロヌマに引き込むツモリは毛頭ありません．御諒謝ください．

　　　　３次元の正投象された４次元図形の特性の一部を紹介．

［３］「投象で失われた情報は脳ミソで補う」

　４次元図形を我々３次人が見られるようにするには，投象して１次元情報量が減っても止むを得ません．減った分は脳ミソで補います．

　　　　正投象ということ．　　　　アタリマエだが基本原理なので小学生語に翻訳します．

［４］「正投象では１回につき１次元しか下げられない」

　２次元の正□はある方向から見ると一線には見えますが，どのように見ても１点には見えません．また対辺のペアは併行（parallel）を保っています．３次元の立方体は正□には見えますが，一線に見えることはあり得ません．投象とはその方向のベクトル成分を０にすることなのですから１回の投象ごとに１次元ずつ下に見るのが限界です．

［５］「球状配置を投象するとドノように見えるか」

　４次元の正（準正）多体胞を３次元に投象したものは，内部構造をもった多面体になります．

［６］「北極から飛び立った航空機を北極星から見ると」

　この見え方をイササカ冗長ですが判り易いように丁寧に述べます．思考的類推の前提として一先ず，３次元で考察しますと北極から３６０機の航空機がそれぞれ角間隔１度で南極に同じ速度で出発することを想定して「これを北極星から見ていますと」次第に機首から尾端までの全長が短くなり，赤道の上空で機体の首尾長が０に見え，また３６０機をつなげた円環はもうこれ以上は拡がりません（出発点を図心と考えます）．地球が透明であれば，その後は機体の長サは回復してきますが，機頭が中に向いています．我々は南半球だから当然だと理解しますが，北極星では機体の長サが縮みながら円環配列が限界半径まで拡がって，再び伸びながら図心に戻るダケのように見えます．その間中も機体の幅は一定に見えています．航空機の場合は重力によって機体が地球的な水平に保たれている物理力によると貧解されないように，幾何学で復習すれば，円盤を敷き詰めていっても同様にダ円にヒシャゲて終には直径ダケ線に見えるノダと言い換えられます．飛行船の如き進行方向に対称形では機頭方向の反転は判然としません．気球なら円に見えたママです．

［７］「図心を直視した場合は歪みなしに見える」

　地球の中心と航空機を結ぶ線上から見れば，恒に形は変化しません（アタリ前ダ）．この無変形視も４次元では重要なので特言します．

［８］「余緯度は縮率と図心距離を与える」

　北極を０度，赤道を９０度とする角度を余緯度θと称します（出発点の図心を０で表したいノデ）．

　北極星から見たとき

　　ａｒｃｓｉｎ（図心−面心）距離／限界半径

　＝ａｒｃｃｏｓ（その場所での機体の長さ／図心での機体の長さ）＝θ

なる位置と大きサを一方が判れば他方が計量できます．（４次元の場合は面心→体心，限界半径→平縮半径となります．）

［９］「中界より先」

　前記をバネにして４次元を推考します．今度は１点から上下方向を含めて３次元的に１度の角間隔で飛び出して，限界半径で球面状に配らんでいます．赤道という語はもう使えないので「中界」と称します．ここから出発点に戻るように見えますが，実は別の場所で前記の南半球の４次元版です．

　　北極→北半球→赤道→南半球→南極　　と言っていたのを，

　　図心→前界→中界→後界→対図心　　　とでも言いましょうか．この場合でも図心を正面にするとそれと垂直な平面では原形を保ったママであることも同様で，ただ厚ミだけが変化しているように投象されています．

［１０］「単胞は中界まで」

　なお，単胞では前記の南半球や後界は在りません．中界や赤道で止まりです．だから単胞simplexと言うのです．

［１１］「単胞の宗値」

　４次元単胞は５点・１０線・△１０壁・△錐５体の図形です．次に述べる触数は４射・６葉・４吊，３枚・３室，２重です．（立体ペンタグラム単胞の３次元への投象です），（１壁は表裏に２ツの面を持つので，言い分けて壁というのです）

［１２］「触数と点囲図，投象でない別の次元低下の方法」

　いずれの点からも４線がでています，４射と称します．また６ツの△壁の角が会します，６葉と称します．さらに４ツの△錐の頂が寄っていて，４吊と称します．これらを総称して触数と言います．この４射−６葉＋４吊＝２と計算するとオイラー則であるので射・葉・吊を頂稜面の数として作った３次元の多面体を点囲図(vertex figure)と言います．さきのいずれかの点というのはこれが中心に在るのだと心眼で想定して（３次元多面体だから中は空）そこから点囲図の頂に線が行っているノダと規定します．ですから点囲図の頂は点ですが１ツの線を表示しています．同様に稜は壁を表示します．壁が△ならこの稜上に３or△と書き込んでおきます．同じく点囲図の面は体の形態を表示します．点囲図の面形が△なら３集体（１頂に３ツの面or３稜が会している多面体，△錐や立方体，正１２面体など）を，□なら４集体（正８面体など），☆なら５葉体（正１２面体など）というｎ集体であることを形で示しています．稜の上の書き込んだ文字が４・６・８という様に面を囲んでいればこの面は４６８という多面体を表示しています．これはまた投象とは別の「次元を低下して考える」方法なのです．

　また１ツの線に属する壁と体の数を「枚」「室」と称します．４次元の正多体胞では両者は等しいのですが，準正多体胞や５次元以上では異なる場合もあります．１ツの壁に接する体を「重」と称します．４次元では恒に２であり，多面体の稜が両側に２ツの面の辺が在ることに相当します．

［１３］「２面角・２体角，視方向の変換」

　立方体はその外形である□を直視できます．方向に注意して２面角だけ回転すれば隣の面が正面に来て，操り返せば全６面が見えます．正△錐の２面角は

　　７０°５２８７７９３６６＝ａｒｃｃｏｓ（１／３）

です．

　４次元の単胞も投象角を７５°５２２４８７８１４換えれば，次々に５体の全部を同じ形に見られます．図心に据えれば歪みのない形で見られます．この角を２体角（他書では胞角）と言い，ｎ次元単体（広義の△）では

　　ａｒｃｃｏｓ（１／ｎ）

です．３次元の投象されたものを２体角や他の角度や毎回異なる角度にしてもダメです．

［１４］「５頂or５面である多面体の吟味」　別図を参照して下さい．

　正多面体ではありませんので３次元空間に均等な角間隔で５本の矢を射出することは不可能です．正２０面体の面心or正１２面体の頂は２０で，頂は３０ですので，５の倍数ですから１／４や１／６を適当に選んでもできません．４次元の単胞が点や体が５ダカラと言っても，３次元に投象してしまえばそれぞれを公平に同じ形に５回見られる模型は作れません．

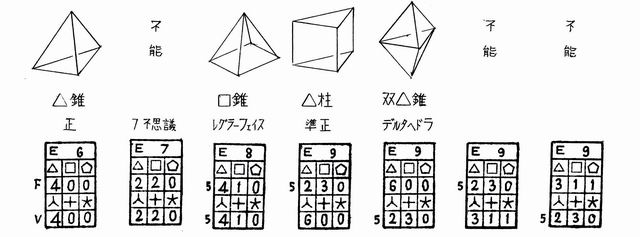
［１５］「△□☆が同数づつ揃っている多面体」

　オトベ著：多面体辞典(1982.2.17完成)未刊より抜粋

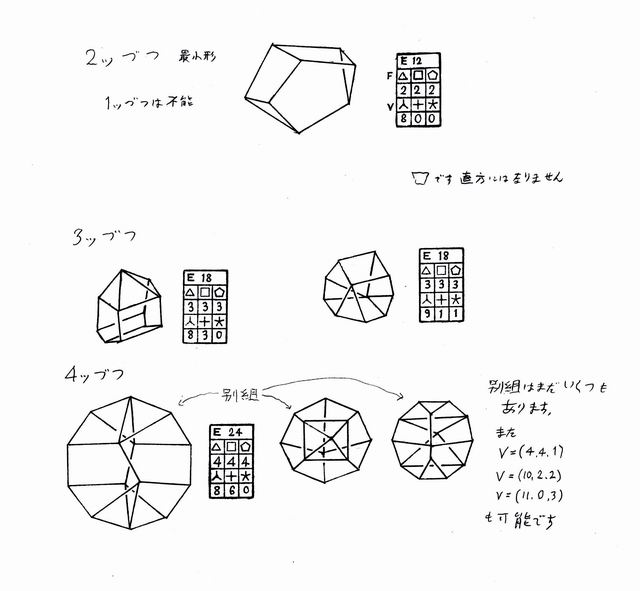
［１６］「立体ペンタグラムは同じ図形が４回見える」

　モウ既に３次元になっていますので，正☆や正△に見える方向は４回です．１ツの壁は表と裏の２面をもつので，中央の１壁をチョウド正△に見えるように，左寄りと右偏りの斜視で４回なのです．☆は実壁ではなく単なる点の配置に過ぎませんが同様です．

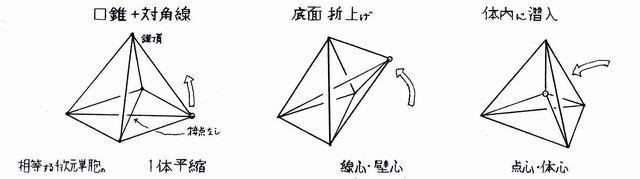
［１７］「□に対角線を追加して多体胞を得る」

　□錐の底面には対角線が引け，線数は単胞と等しくなり，対角線１ツの両側で△２ツ，錐頂を含む△１ツが新生し，対角線は２ツなので元のと合計して１０△となり単胞とツジツマが合います．広義の△に１点を追加して次元を上げるのとはやや趣が異なる考え方です．また立方体の６□面に１２対角線を追加したものは偶胞（他書では１６胞）の正投象の体心図そのものです（その他省略）．

［１８］「立体ペンタグラムの構想の意企」　　（当用漢字では意図に改悪されたが今回は図では誤解されそうナノデ）

　４次元を扱うテキストの初頭には必ず完全グラフの結線として図示されているケレド，紙上なので見かけの交点が生ずるのはヤむを得ませんが，そこは結点では無イんダ！ということを明示したかったので，工夫したものです．正△は本来の図形ですので１ツダケでも顕在させ，その結果□も出現したので始メッから△□☆を揃えるというオブジェのような稽術的作品ではありません．重複して数が減るダケの「お化け煙突」より視方向での変化は強烈です．お化け煙突」を意識したことはありませんが，ウマイ譬喩です．

［１９］「抽象とは図なしのことダった」

　抽象とはそういうことダッタのか．　投象法のテキストは判りづらい数式繁多でたいへん抽象的です（文字通り抽象とはこのことカ，ナルホド）．これでは数式アレルギーの人は読んでくれるのカナ．数式の羅列はそれはそれで必ず正しいのですが計算が終わるマデにイメージが浮かぶのは一松先生のような大家のみカナ．

［２０］「図形で考えた時代」

　ギリシア幾何の頃には代数やデカルト座標も無かったのに，彼等は図形で考察して奇怪学を大成しました．私はこれこそ戯画学の本質であると思っています．小生の方法では始ッから見えていました．後図でそのプロセスをタネアカシします．

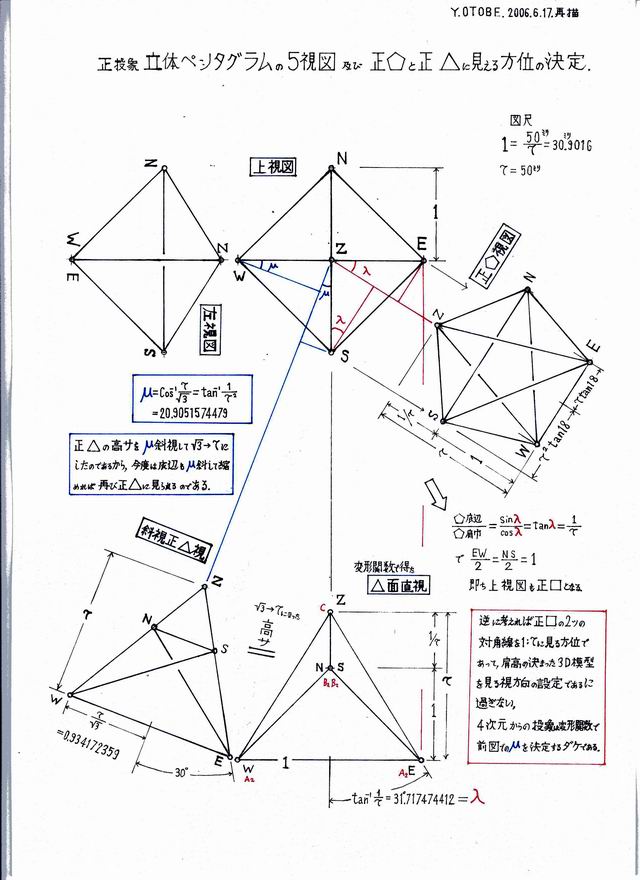
［２１］「変形関数は図形であって数式ではない」

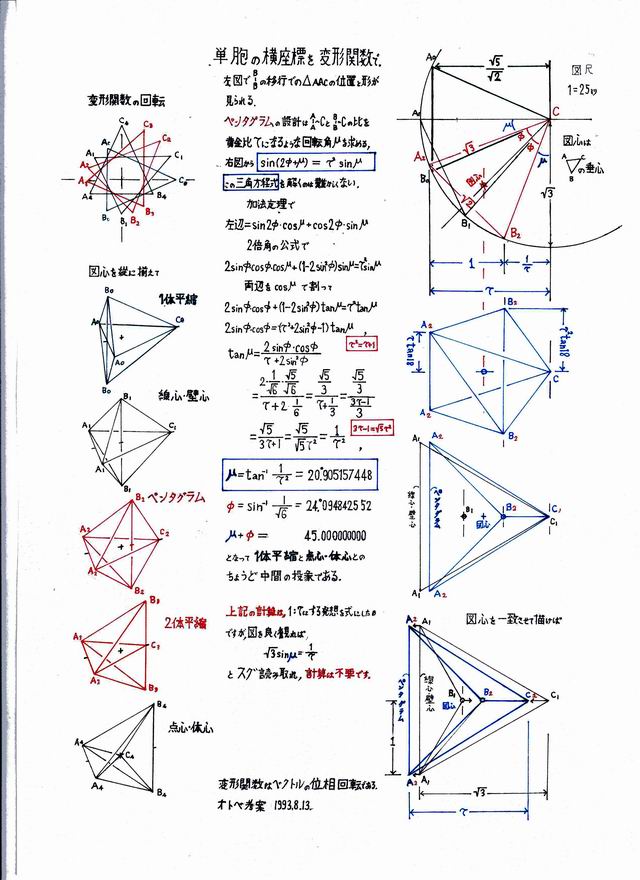
　勿論，座標を回転変換する数式計算法は確立していますが，図形のある部分を移動させると，他の部分がどういうふうに変形するか途中経過をも簡単にかつ直観的に解明できるように考案したのが，回転して用いる変形関数という幾何学的な構想です．図心は変形関数の垂心に固定しています．これまで計量的にはあまり意味をもたなかった垂心も脚光が与えられることになりました．変形関数で立体ペンタグラムを正確に設計できることを別紙の図面で見て下さい．モウ駄文はイラナイでしょう．

［２２］「宇宙が手に載せられる」

　相対性理論で運動物体が光速度になると長さが０になるということ．観測天文学が発見した宇宙膨張との関係を［６］での理由で４次元多体胞の正投象模型の中で見て取れますが，図形の学問にすぎない幾何が宇宙の姿の理論と事実を与えているのは驚きです．この話は別の機会にします．４次元の幾何学はマダ死に学問ではないのです．

［２３］「お別れのアイサツ」

　これまでワザと第４番目のＵ軸という語を避けてきました．Ｘ-Ｙ-Ｚ軸などの座標を言いませんでした．図面と拙文からそれが何処にあるかを考え出していただくように抽象化を退けて具体的な脳内イメージを喚起するように配慮したツモリです．私の作った図面や模型は判り易いが，数式より難解だと言われたことがある「駄文」を読了していただいて御礼申し上げます．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［後記］

　４次元幾何学に関わる基礎を解説していただいたが，乙部氏の記述は意味不明ではないにしても仏教用語に似た独自の用語も多く，その点はとっつきにくかったかもしれない．

　まず，氏は「多胞体」と呼ばずに「多体胞」と呼んでおられる．面は２次元，体は３次元，したがって胞は４次元に使う用語であるべきということを主張しているわけである．同様に，

　　頂点・辺（稜）・面・胞　→　点・線・壁・体

　正多面体の各面を正ｐ角形，各頂点にｑ面が会するとして，その頂点数，辺数，面数を（ｖ1，ｅ1，ｆ1）としよう．正多面体（ｐ，ｑ）を境界多面体とする４次元正多胞体では，頂点に集まる辺の中点を結んでできる多面体を頂点図形：ｖ2，ｅ2，ｆ2）と呼ぶことにすると，それはｑ角形が１つの頂点にｒ面会した多面体（ｑ，ｒ）になっている．

　　（ｖ2，ｅ2，ｆ2）　→　射・葉・吊

　　（ｐ，ｑ，ｒ）　　→　枚，室，（重）

境界面ｐ，頂点に集まる面ｑ，辺に集まる胞ｒであって，重はｒとは異なる．このような置き換えを行えば，摩訶不思議な教典もあながち解読不能ではないはずである．

　幾何学に王道なし，たとえ一国の王といえども努力しないで数学を習得するための近道はなく，自分の足で目的地へ到達しなくてはならないのだ．幾何学が苦手な読者はじっくり時間をかけて読むことを勧める次第である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝