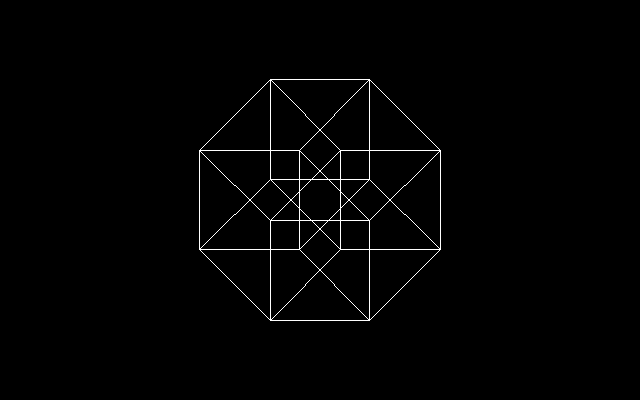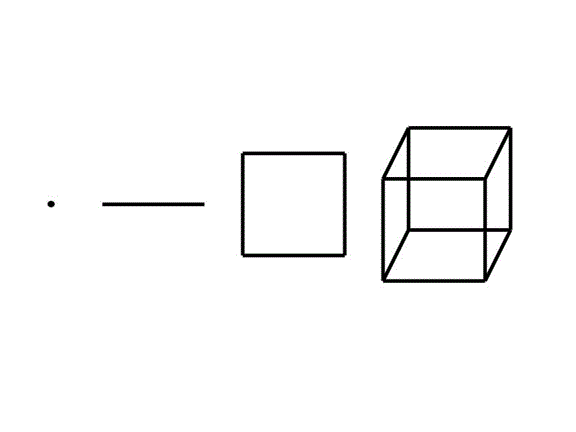黄金比は正五角形と密接な関係にある．正五角形に対角線を書き入れると星形五角形できるが，この手順を繰り返すと，正五角形と星形五角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができる．正五角形に対角線を描き入れると星形五角形（ソロモンの星）ができるが，正五角形と星形五角形の入れ子はペンタグラムと呼ばれる．この図形が４次元正単体の２次元投影図であることを知っている人は少ないだろう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】３次元立方体の投影図

　３次元立方体を（１，１，１）方向に投影すると，２次元投影図は正六角形になる．

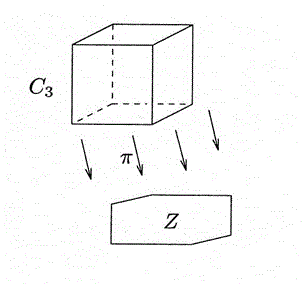
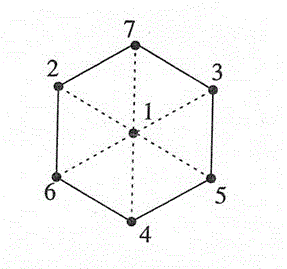
　最近の若い人の中には，この図を見て「三角形が６つ合わさった形」と答える人がいるとのことである．この答えは間違いではないが，立体図形に見えないのなら少々問題があるだろう．

　以下のロゴは，東北大学金属材料研究所のものであるが，正六角形の対角線のなかで対頂点を結ぶ対角線３本がはいっている．川添良幸先生から聞いた話では「この六角形が立方体に見えぬ者はこの門をくぐるなかれ」といったことを意味しているそうである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】４次元立方体の投影図

　白銀比は正八角形と密接な関係にある．正八角形に３／８角形を書き入れると正八角形できるが，この手順を繰り返すと，正八角形と星形８／３角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができる．ところで，この図形は４次元立方体の３次元投影図でもある．

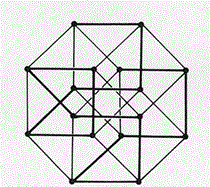
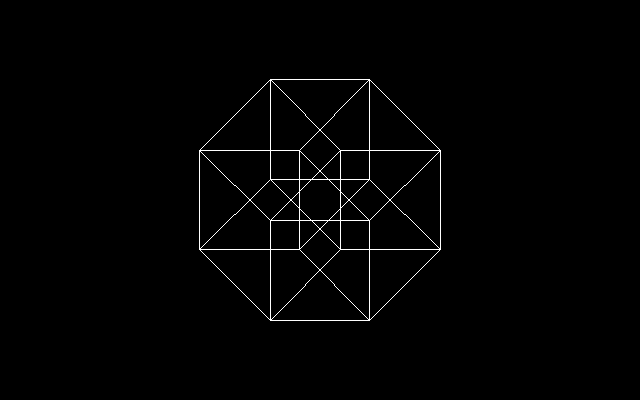
　３次元立方体の８つの頂点を第４の方向に１単位だけ平行移動することにより，４次元立方体の３次元投影図を描くことができる．

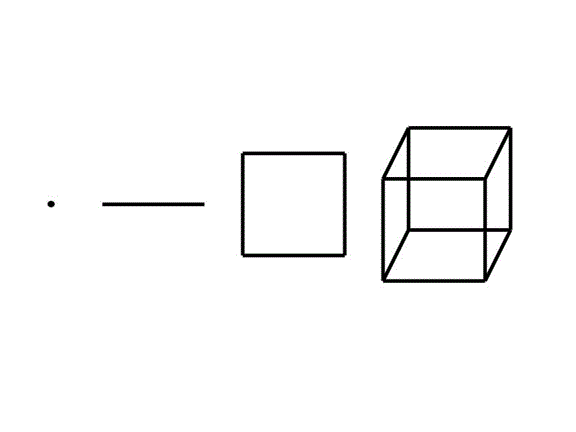
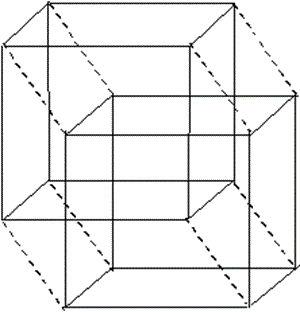
　以下にイメージミッション社のロゴを掲げるが，この図が何を要求しているのか，会長の前畑謙次さんに窺いたいところである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝