面心立方格子と体心立方格子を仲介するメカニズムが存在する

ここではフリップ・フロップ 変身図形についてみてみたい　　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

デュドニーは正三角形が一瞬にして正方形に等積変形するパズルを提案した．その際，正三角形の表面は正方形の内部に移り，正方形の表面は正三角形の内部の点から構成されている．

それは２次元変身の例であるが，３次元図形である平行多面体でもこのような表裏翻転が可能であることが示される．

［定理］１５通りあるすべての平行多面体の対の間で，平行多面体同士のフリップ・フロップ変身が可能である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
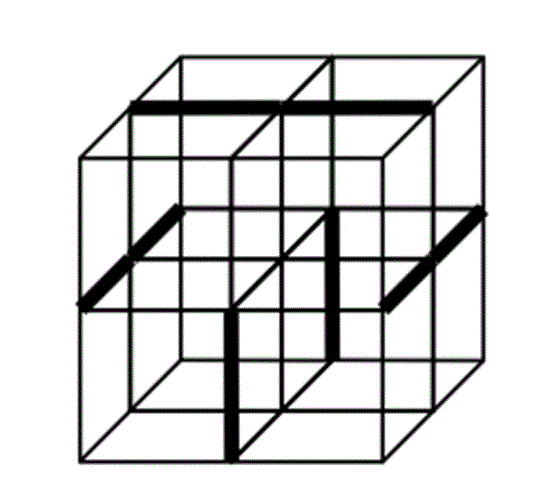
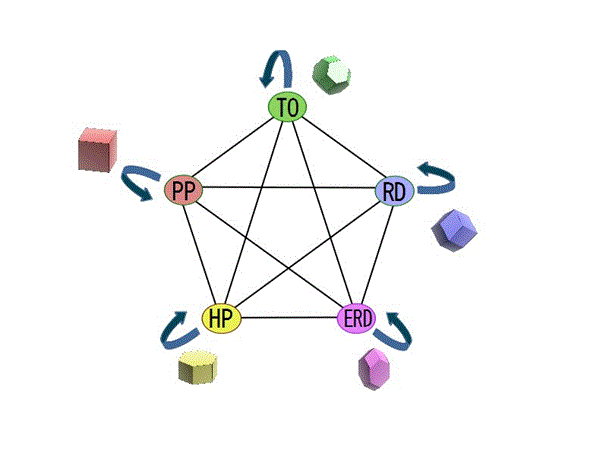