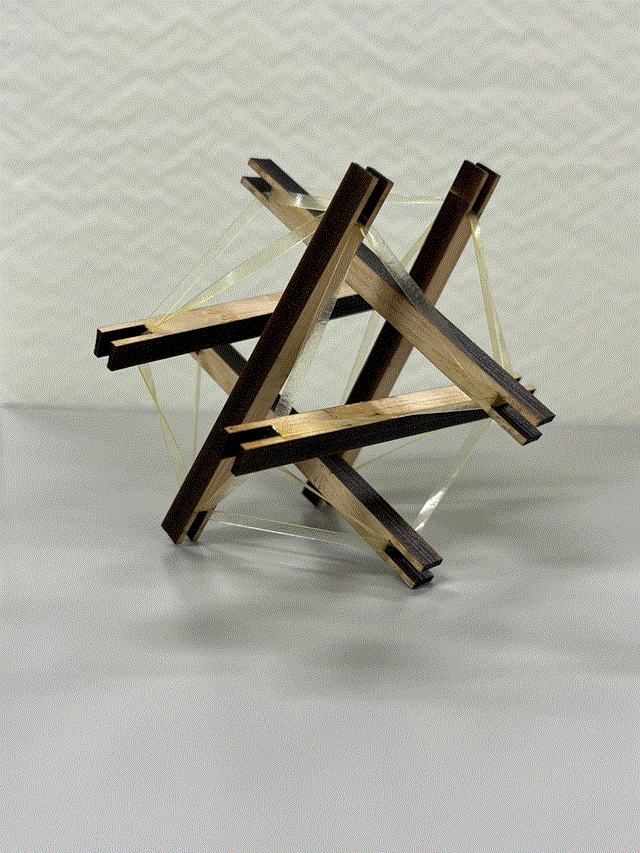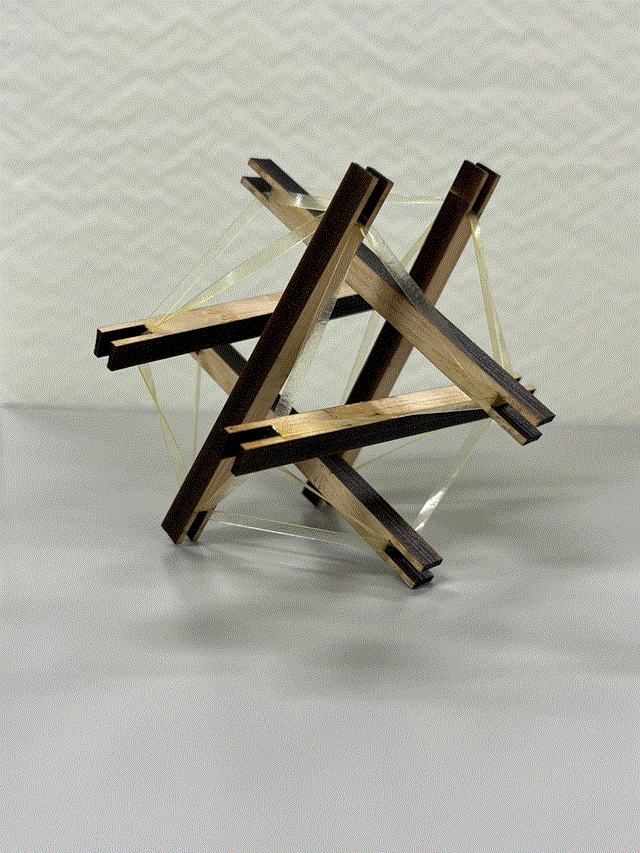テンセグリティ構造（張力統合体構造）とはフラーが張力(tension)と統合(integrity)から作った造語である。彫刻家のスネルソンによって考案された棒とひもの組み合わせによる構造で、フラーによって広められた。おそらく、最初のテンセグリティ構造は帆船のマストと船の先端・船尾をロープでつないだ構造であったと思われる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】６本の矢

正２０面体の黄金比に関する性質を利用して、正２０面体のテンセグリティ・モデルを創生することができる。以下の写真は山�ｱ　憲久さん（積み木インテリアギャラリー）による「６本の矢」からなるもので、単位立方体のそれぞれの面に長さφの木を直交３方向に配置したものである。合計１２個の矢の端点を輪ゴムでつなぐと、正２０面体が出来上がる。正２０面体を形作る３０本の辺の中には冗長なものがあるので、それを取り除くと２４本の辺だけである。輪ゴムを使って空間菱形ができるように頂点を連結するのである。結局、６本の木に対して６個の輪ゴムを使うことになる。（この説明には誤りがあります)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

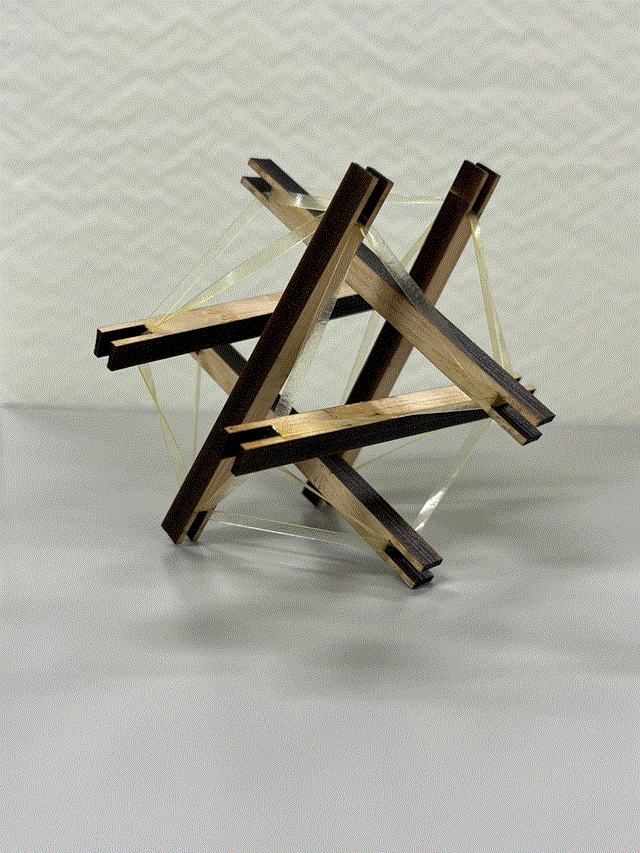
６本の矢は「イエッセンの２０面体」と言われていますが、どのように計算するのか教えていただけるとうれしいです。（山�ｱ　憲久）

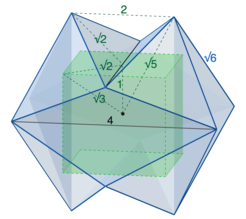
正２０面体を非平面菱形に置き換えた非凸多面体になっていただけなので、計算は簡単です（佐藤郁郎）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

力学的に、棒と輪ゴムの質量をゼロとみなせば、伸び縮する輪ゴムを使えばどこに落ち着きますか？（山�ｱ　憲久）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

直観的には正20面体になる気がしますが、計算で確認してみます

A(d,0,1)

B(1,d,0)

C(0,1,d)

ベクトルの大きさをD={(d-1)^2+d^2+1}^1/2として

ABのｘ方向の成分は(d-1)/D

ACのｘ方向の成分はd/D

これらが釣り合うからd=1/2

正20面体であると思っていたのですが、釣り合いの位置は、棒の長さの半分で上図の通りになりました。（佐藤郁郎）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（訂正）上の写真は山�ｱ　憲久さん（積み木インテリアギャラリー）による「６本の矢」からなるもので、辺長2の立方体のそれぞれの面に長さ4の木を直交３方向に配置したものである。合計１２個の矢の端点を輪ゴムでつなぐと、「イエッセンの２０面体」が出来上がる。「イエッセンの２０面体」を形作る３０本の辺の中には冗長なものがあるので、それを取り除くと２４本の辺だけである。輪ゴムを使って空間菱形ができるように頂点を連結するのである。結局、６本の木に対して６個の輪ゴムを使うことになる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝