θ=π/n、m=(n-1)/2として、

(1,R)を焦点とする楕円・放物線・双曲線(x^2/a^2+y^2/b^2=1,y^2=4px,x^2/a^2-y^2/b^2=1)を求めたい

軸はy=tan(mθ)x

(1.0)を通るためにはy=-1/tan(mθ)・(x-1)との交点を求める

{tan(mθ)+1/tan(mθ)}・x=1/tan(mθ)

{tan(mθ)^2+1}/tan(mθ)}・x=1/tan(mθ)

x=cos(mθ)^2

y=cos(mθ)sin(mθ)・・・ここを焦点とする楕円を考える

(x,y)から(0,0)までの距離は

{cos(mθ)^2}^2+cos(mθ)^2sin(mθ)^2＝cos(mθ)^4+cos(mθ)^2sin(mθ)^2

=cos(mθ)^2

よりcos(mθ)

(x,y)から(1,0)までの距離は

{cos(mθ)^2-1}^2+cos(mθ)^2sin(mθ)^2＝sin(mθ)^4+cos(mθ)^2sin(mθ)^2

=sin(mθ)^2

よりsin(mθ)

この1/2がｐになるからp=sin(mθ)/2

放物線の頂点は

x=cos(mθ)^2-pcos(mθ)=cos(mθ){cos(mθ)-sin(mθ)/2} ＜0

y=cos(mθ)sin(mθ)-psin(mθ)=sin(mθ){cos(mθ)-sin(mθ)/2} ＜0

(0,0)から(x,y)までの距離は|cos(mθ)-sin(mθ)/2|

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

(1,0),(cos2mθ,sin2mθ)を通る。

(x,y)を標準的な座標(x^2/a^2+y^2/b^2=1,y^2=4px,x^2/a^2-y^2/b^2=1)とする

y^2=4px,x=pt^2,y=2pt,(p+α)^2=1+R^2であってp^2=1+R^2ではない

(x1,y1)における接線はy1y=2p(x+x1)

y=0→x=-x1

(-x1,0)から(x1,y1)までの距離は1・・・4ｘ^2+y^2=1

R=tan(mθ)=cot(θ/2)

cos(mθ)=sin(θ/2)

sin(mθ)=cos(θ/2)

y^2=4pxをy=tan(mθ)を軸とする放物線に写したい。

円の場合は(1,R)が焦点、(1,0),(cos2mθ,sin2mθ)が接点となっていた。両方を同時に満たすことを考える

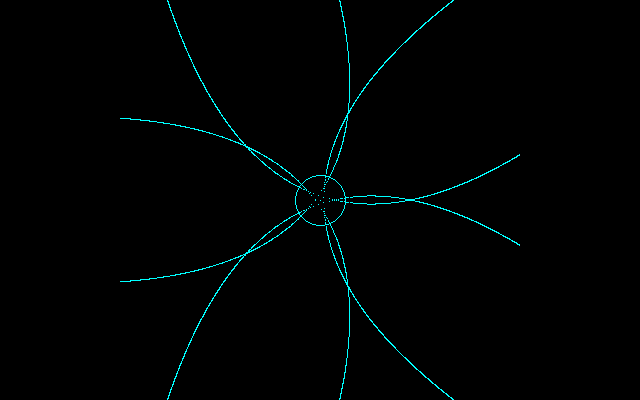
図を描いてみると両方を満たすことは不可能なのかもしれない・・・

焦点が(1,R)がないと面積計算は難しい

一方、接点が(1,0)にないと面積が大きくなってしまう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

(x,y),[X,Y]

X-α=[cosmθ,-sinmθ][x]

Y-β=[sinmθ, cosmθ][y]

[一方、焦点が(1,R)、(1,0)を通るという条件だけを使うと]NG

y^2=4px

(0,0)→[α,αtan(mθ)]=[α,β]=[qcos(mθ),qsin(mθ)]

p+q=(1+R^2)^1/2

(p,0)→[1,R]

(p,-2p)→[γ,δ]=[pcos(mθ)+2psin(mθ),psin(mθ)-2pcos(mθ)]

psin(mθ)-2pcos(mθ)＞0となるのは、tan(mθ)＞2

(n-1)/n・π/2＞arctan(2)=1.10715

(n-1)/n＞0.704833

n>4ならばこれを満たす。(1,0)を下から上に通過する可能性が高いが、(1,0)を接点にすることは可能かもしれない。

n=3のとき(1,0)を上から下に通過する

しかし、この点を通っていないので、どこかに誤りがあることは確かである。→モニターのスケール外でこの点を通ることがわかった。したがって、描画プログラムは正しく作動している

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

接点となるならば

[(x1,-y1)→[1,0],y1＞0]・・・(1.0)を通るならば

[(x1,y1)→[cos2mθ,sin2mθ]]

[(-x1,0)→[0,0]も必要である]・・・さらに接点となるならば、これらの条件が必要になる。

(x,y),[X,Y]

X-α=[cosmθ,-sinmθ][x]

Y-β=[sinmθ, cosmθ][y]

p,α,β,tは未知数、Rは既知

1-α=cosmθ・p

R-β=sinmθ・p・・・R=tan(mθ)と同値

1-α=cosmθ・x+sinmθ・y

0-β=sinmθ・x-cosmθ・y,y＞0・・・(1.0)を通るならば

cos2mθ-α=cosmθ・x-sinmθ・y

sin2mθ-β=sinmθ・x+cosmθ・y,y＞0

α=cosmθ・x

β=sinmθ・x・・・さらに(1,0)が接点となるならば、これらの条件が必要になる。・・・ここまではあっていると思われる。

1+cos2mθ-2α=2cosmθ・x→2(cosmθ)^2-2α=2cosmθ・x

1-cos2mθ=2sinmθ・y→2(sinmθ)^2=2sinmθ・y→y=sinmθ

sin2mθ-2β=2sinmθ・x→2sinmθcosmθ-2β=2sinmθ・x→2sinmθcosmθ-2αtanmθ=2sinmθ・x→2(cosmθ)^2-2α=2cosmθ・x

-sin2mθ=-2cosmθ・y→2sinmθcosmθ=2cosmθ・y→y=sinmθ

(1,0)が接点となるための条件である

α=cosmθ・xを代入すると2(cosmθ)^2=4cosmθ・x

x=(cosmθ)/2, y=sinmθ

α=(cosmθ)^2/2（合致）

β=sinmθ・(cosmθ)/2（合致）

p=1/cosmθ-(cosmθ)/2（合致）・・・p=(1+R^2)^1/2-α(1+(tanmθ)^2) ^1/2=(1-(cosmθ)^2/2)/cosmθ

x=pt^2,y=2pt

x/y=t/2

t=1/tanmθ

このとき

4x^2+y^2=1

になっているのだろうか？　

x=(cosmθ)/2, y=sinmθであるからOK

結局、計算が簡単になっただけで、結果は変わらない。・・・ここまではあっていると思われる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

(1,0)を通り、かつ,その点が接点になるように設定したが、そうはならない。

条件を(1,0)を通るだけにすればどうなるのだろうか？

1-α=cosmθ・p

R-β=sinmθ・p・・・R=tan(mθ)と同値

1-α=cosmθ・x+sinmθ・y

0-β=sinmθ・x-cosmθ・y,y＞0・・・(1.0)を通るならば

cos2mθ-α=cosmθ・x-sinmθ・y

sin2mθ-β=sinmθ・x+cosmθ・y,y＞0、ｘ軸をまたぐ点は２点ある

1+cos2mθ-2α=2cosmθ・x→2(cosmθ)^2-2α=2cosmθ・x

1-cos2mθ=2sinmθ・y→2(sinmθ)^2=2sinmθ・y→y=sinmθ

sin2mθ-2β=2sinmθ・x→2sinmθcosmθ-2β=2sinmθ・x→2sinmθcosmθ-2αtanmθ=2sinmθ・x→2(cosmθ)^2-2α=2cosmθ・x

-sin2mθ=-2cosmθ・y→2sinmθcosmθ=2cosmθ・y→y=sinmθ

αが求められればよいのであるが、この条件だけでは一意に決まらないので無理であろう

一意に決まるのは円だけのようである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

接線がｘ軸と平行になる点は1点だけである。この点を(x1,y1)とする。

y^2=4px

2y・dy/dx=4p

dy/dx=2p/y=-tan(mθ)

y=-2p/tan(mθ)

x=y^2/4p=p/{tan(mθ)}^2

この点が(1,0)になるためには

4x^2+y^2=1を満たす必要がある。

4p^2/{tan(mθ)}^4+4p^2/{tan(mθ)}^2=1

p^2=1/4・tan(mθ)^6/{tan(mθ)^4+tan(mθ)^2} ・・・ｐはかなり小さくならなければならない。→面積が大きくなる

tan(mθ)=2としても

p^2=1/4・64/20〜3/4

tan(mθ)=4とすると

p^2=1/4・4096/272〜15/4

いずれにせよNGであることは図を見れば理解できる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

p^2＜1+R^2=1+{tan(mθ)}^2

tan(mθ)=2,p^2＜5

tan(mθ)=4,p^2＜17

放物線の頂点は円外になってしまうかもしれない

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝