こんどは綿棒多面体の菱形３０面体の核についてです。

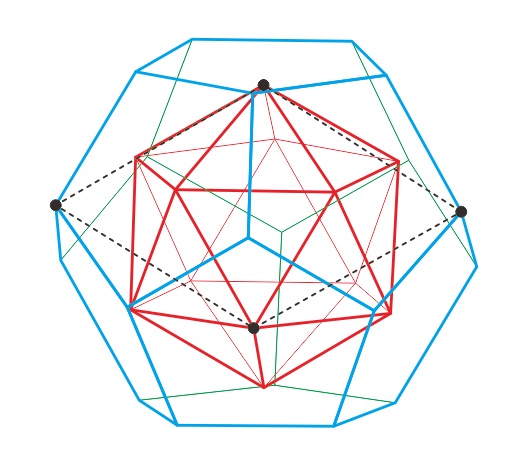
正十二面体の頂点と、その双対の正二十面体を１０％強縮小したものの頂点を使います。頂点Aから正十二面体の天面までの距離＝頂点Aの対頂点A'から正十二面体の底面までの距離で、正十二面体と正二十面体の重心は一致しています。

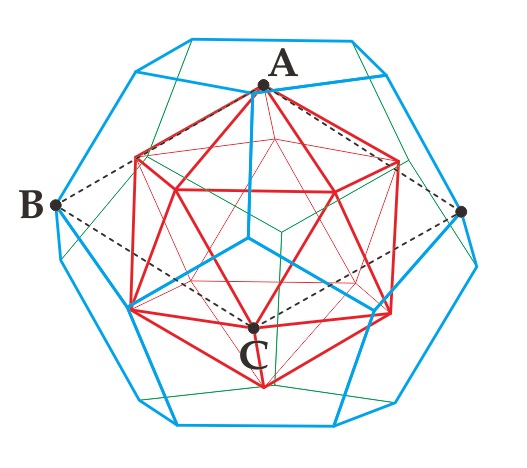
このとき、正二十面体の頂点Aー正十二面体の頂点Bー正二十面体の頂点Cのなす３次元空間における角度が黄金菱形、菱形３０面体の菱形と同じになるのは、正二十面体をどの程度縮小したときでしょうか？　　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　φ^-4＝−３φ＋５、 √５φ^-4＝７φ−１１

　　φ^-3＝２φ−３、 √５φ^-3＝-４φ＋７

　　φ^-2＝−φ＋２、 √５φ^-2＝３φ−４

　　φ^-1＝φ−１、 √５φ^-1＝−φ＋３

　　φ^0＝１、 √５φ^0＝２φ−１

　　φ^1＝φ、 √５φ^1＝φ＋２

　　φ^2＝φ＋１、 √５φ^2＝３φ＋１

　　φ^3＝２φ＋１、 √５φ^3＝４φ＋３

　　φ^4＝３φ＋２、 √５φ^4＝７φ＋４

　　φ^5＝５φ＋３、 √５φ^5＝11φ＋７

　　φ^6＝８φ＋５、 √５φ^6＝18φ＋11

　右辺ｍφ＋ｎの係数ｍ，ｎはフィボナッチ数列をなす．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

双対のときの縮小率mは

φ^2=m{(φ＋φ^-1)/2+3/2+φ^-1}＝m{(2φ-1)/2+3/2+φ-1}=2mφ

m=φ/2

x:中心軸から左

y:中心軸から手前

z:中心軸から上

さらにμを縮小率とする。μ=mx

A(0,μ(φ^2/2-1),μφ)

C(0,μφ^2/2,-μ)

B(φsin2π/5,φcos2π/5,φ^2/2-1)

AC=(0,μ,-μφ^2)

BB'=(2φsinC,0,0)

φ^2AC^2=4φ^2(sin2π/5)^2

μ^2(1+φ^4)=4(sin2π/5)^2=4(1-1/4φ^2)=(4-1/φ^2)

μ^2=(4-1/φ^2)/(1+φ^4)=(4+φ-2)/(3φ+3)=√５φ/3φ^2=√５/3φ

m^2x^2=φ^2/4・x^2=√５/3φ

x^2=4√５/3φ^3＝4√５/3・(2φ-3)

x=0.838939

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝