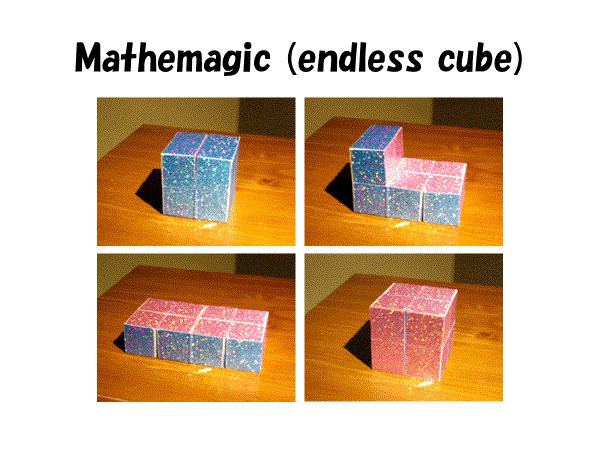デュドニーは正三角形から正方形に等積変形するパズルを考案した．また，３次元ではエンドレス・キューブという立方体同士の表裏翻転図形がよく知られていて，適当な稜が蝶番でつながれた８つの立方体の輪は立方体（２×２×２）に折りたたむことができる．エンドレス・キューブは表の２４面を裏返すと裏の２４面が現れてくることを利用している．

　エンドレス・キューブに観光地の写真を貼り付けてあるおみやげグッズも売られているから，ご存知のかたも多いと思うが，これは最も単純なリバーシブル多面体である．もし，平行多面体はデーン不変量が０であるから、平行多面体間でもこのような変身が起こり得るならば，それは相転移を直接的に表現する模型となるはずである．

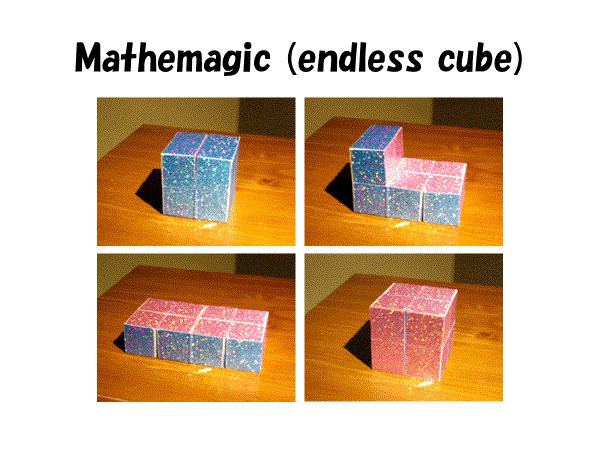
［定理］１５通りあるすべての平行多面体の対の間で，平行多面体同士のフリップ・フロップ変身が可能である．

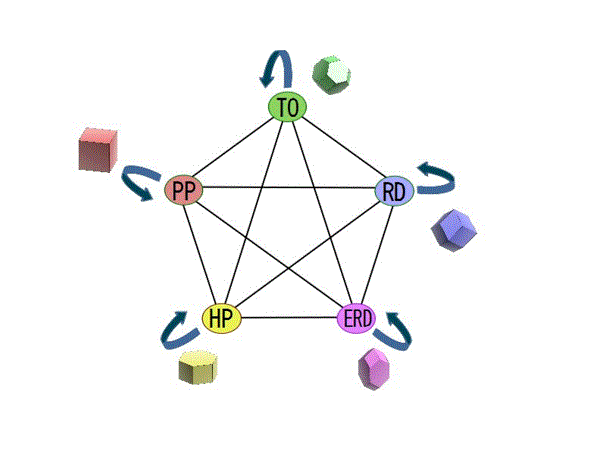
秋山仁先生はこのようなリバーシブルな等積変形多面体をすべて決定する試みをされている．以前，パリ大学で行われた秋山先生の変身多面体の講義は，多くの研究者の関心を集めたようで，中にはアルゴリズムの研究から多面体の研究に鞍替えしたいという若い研究者も現れたぐらいだったそうである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

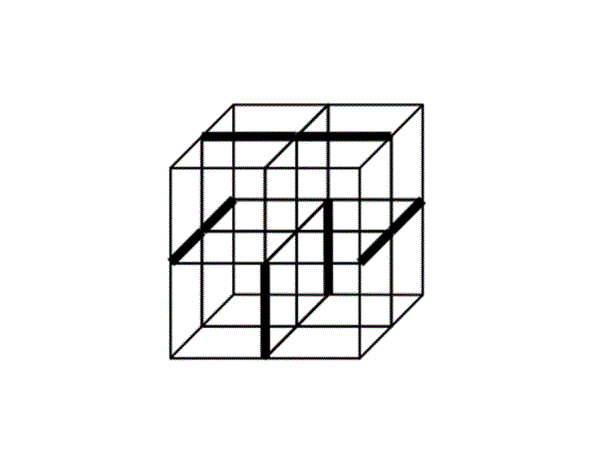
【１】エンドレスキューブのつなぎ方

　直交３方向を東西・南北・天地方向にとる．天面の東西方向の２カ所を繋げる．東面・西面の南北方向の２カ所ずつ，計４カ所を繋げる．南面・北面の天地方向の底面よりを１カ所ずつ，計２カ所を繋げる．底面はそのままにする．　これで，８個の小立方体を８カ所で繋げたことになる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝