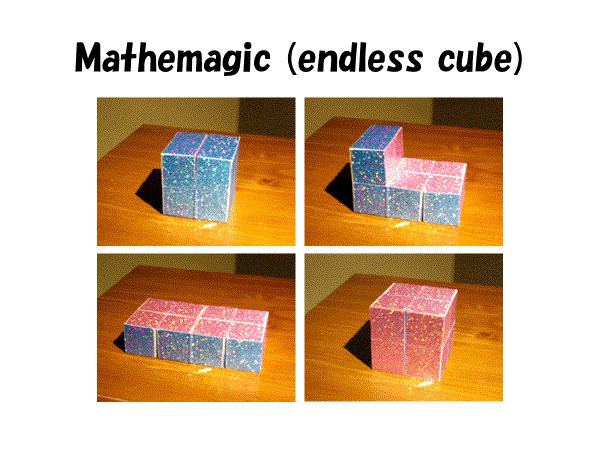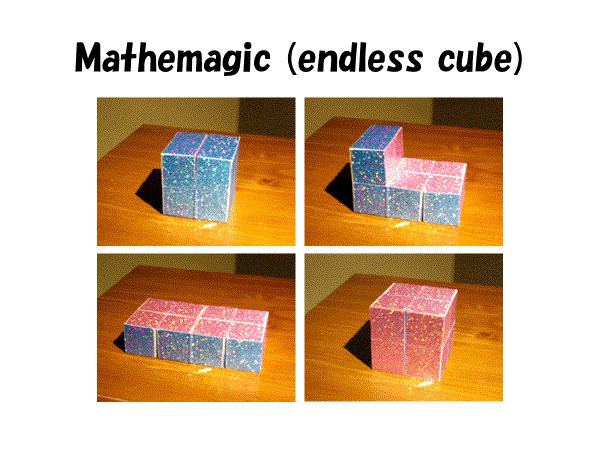観光地の土産物屋で、稜が蝶番でつながれた８つの立方体の輪からなるおみやげグッズを手に取ったことはないだろうか。たとえば，表面２４個にロンドンの観光写真六景を載せていて、それを裏返すと，裏面（隠れている面）２４個にパリの観光写真六景が現れてくる．

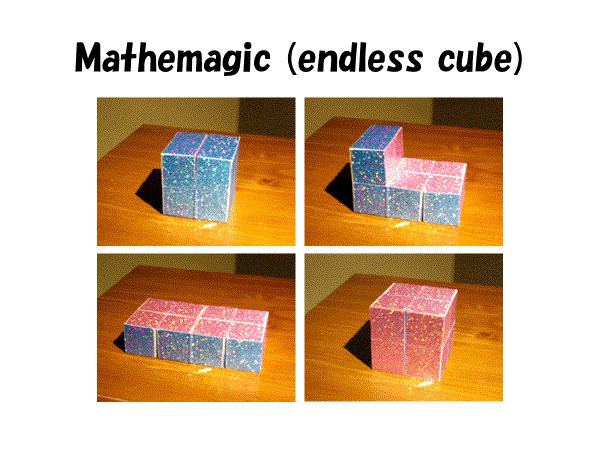
　８個の小立方体を８カ所で繋げると大立方体（２×２×２）に折りたたむことができて、表面２４個にロンドンの観光写真を載せれば，裏面（隠れている面）２４個にパリの観光写真を載せることができるのである．その連結の位置関係は実におもしろく，うまく繋げばバラバラになることなしに，６面×８個＝４８面すべてをみせることができる．これはエンドレスキューブと呼ばれている。ロンドン→パリ→ロンドン→パリ→・・・の回転はエンドレスに続く。

折り紙はガウス曲率が0であることを利用している。変形可能な曲面、平面に展開可能な曲面（可展面）という意味である。一方、エンドレスキューブはデーン不変量が0であることを利用しているのである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

南米の地方空港だったと記憶しているが、土産物屋に絵が描かれている紙が置かれていた。すると突然、店員がその紙をくしゃくしゃにまるめはじめた。驚いたのであるが、もっと驚いたことにその紙は形状を記憶しているかのように再び平面に戻ってしまったのである。

これがパピルスとの出会いであった。古代エジプトでパピルスが利用されていることは知っていたが、実物を見たのはこれが最初だった。古代ギリシャの古文書もパピルスでできているのであろう。反面、パピルスでは折り目がきれいにつくようには折りにくい。折り紙は紙が発明された中世以降に生まれたのであろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝