[Q]

v1-v4,v11-v14は半径√3/2の円上

v5-v10は半径1の円上に投影される→六角形だろうか

P=(x,y,z,w)

A=[a,b,c,d]

[e,f,g,h]

[i,j,k,l]

[1/2,1/2,1/2,1/2]

P=A・v

(x,y)平面に投影したとき、正八角形にすることができると思っていたが、不可能なのだろうか？

行列Aを求めよ

このことに関して

石井源久先生よりメールをいただいた。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

佐藤先生が言われるのは、対角状に位置する２頂点が、２次元上の原点で重なって１点に見える条件の下で、４次元立方体の投影図が、６角形になるような変換行列があるか？ということのように思えますが、そのパターンは確かにあります。図を６つ添付します。

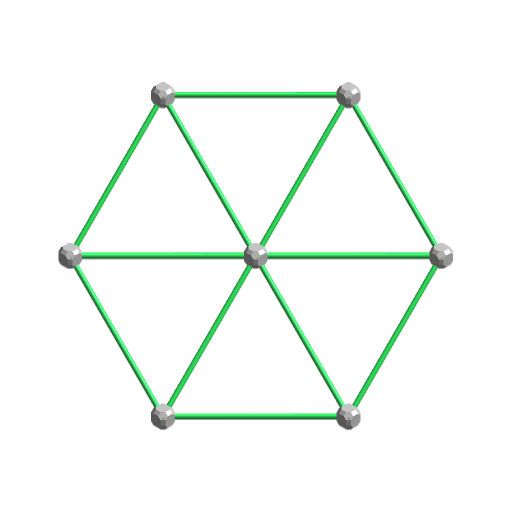
E1は３次元への投影が、正６角柱になるもので、４次元→３次元への投影において「線心図」と呼ばれます。

ある方向から見ると、E0のように正６角形になります。この場合、いくつかの頂点が重なっている位置があります。

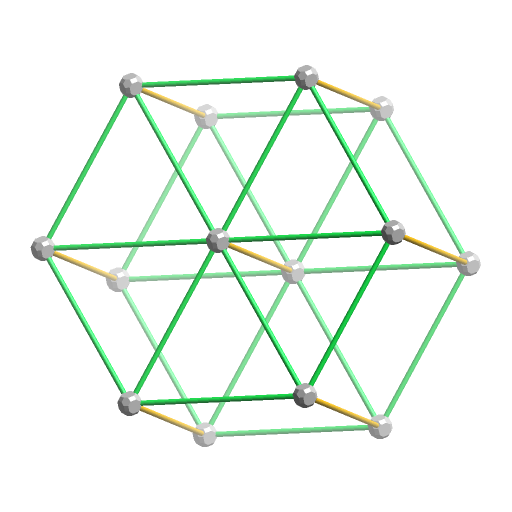
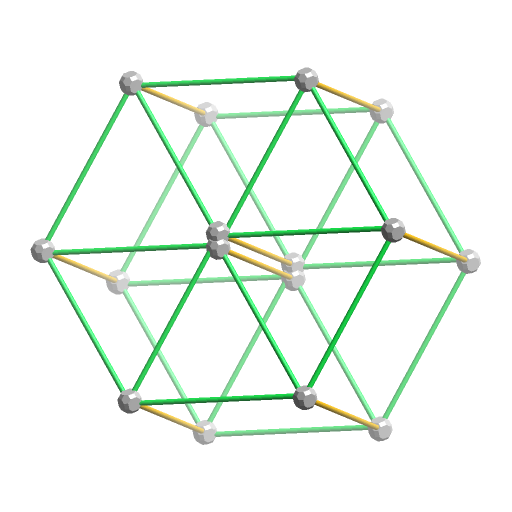
分かりやすいように4次元内で少しだけ回転させた図をE2に示しました。

上底面と下底面になっている正６角形の中心に、２つの頂点が重なっていることが分かります。

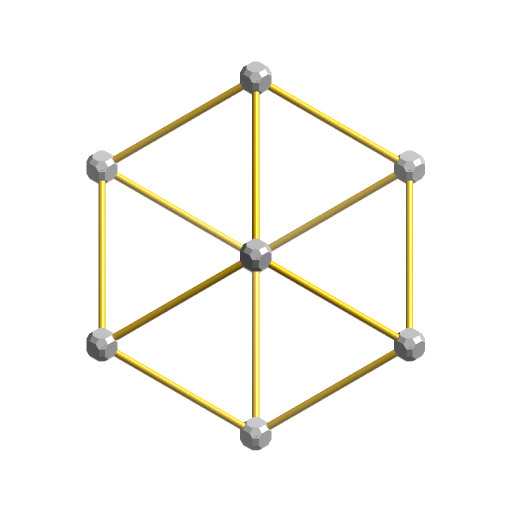
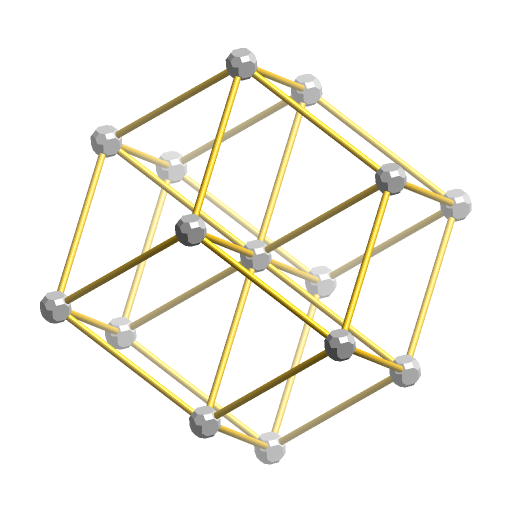
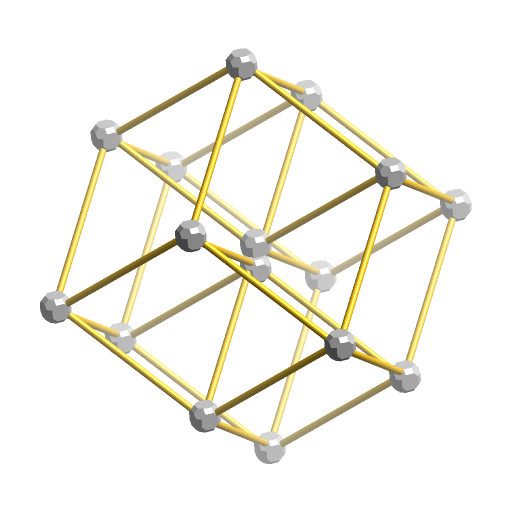
V1は３次元への投影が菱形12面体になるもので、４次元→３次元への投影において「点心図」と呼ばれます。

これもある方向から見ると、V0のように正６角形になります。

これもV2のように４次元内で少しだけ回転させると、中心には２つの頂点が重なっていることが分かります。

それで、佐藤先生の考えられている変換は、V0やV1のようにするものだと思われます。最も手前の頂点がv0で、そこから棒でつながっている１近傍のものがv1〜v4、２近傍のものがv5〜v10、３近傍のものがv11〜v14、4近傍のものがv15ではないでしょうか。

重要なのは、４次元内で回転させた場合には、２次元や3次元での距離が保たれるとは限らないことです。（例に挙げた図では３次元的な距離は保たれていますが、これは特別な場合です。）そのため、v1〜v4のうち１つだけが他の３つが位置する円周上ではなく中心に来ていますし、v11〜v14のうち1つだけが同じく中心に来ています。（v5〜v10については同じ円周上にあります）

この推論で正しければ、[Q]にも、時間のあるとき、お答えすることができると思います。　　（石井源久）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝