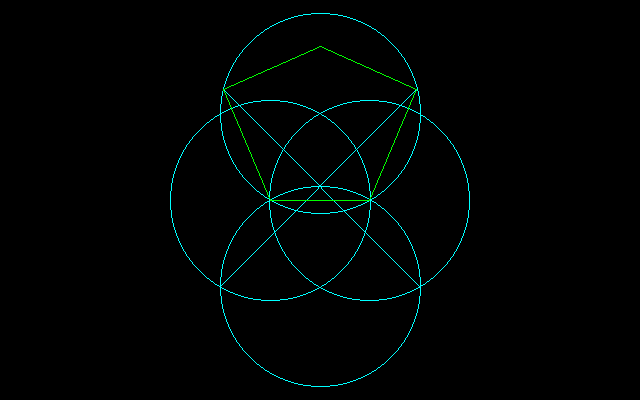
［１］半径が等しく，その中心が互いの円周上にある４円が重なり合った共通部分の両端を点Ａ（−１，０），点Ｂ（１，０）とする．ＡＢが正５角形の１辺の長さとなる．

［２］点Ａを中心とする円を第１円，点Ｂを中心とする円を第２円とする．

［３］第１円と第３円の交点が正六角形の頂点となる．点Ｃ（−２，−√３）とする．

［４］点Ｃと第３円上の点（０，２−√３）を通る直線と第４円の交点を点Ｄとすると，点Ａ，Ｂ，Ｄが正五角形の３頂点となる．

　点Ｃ（−２，−√３），点（０，２−√３）を結ぶ直線は

　　ｙ＝ｘ＋２−√３

　ｘ^2＋（ｙ−√３）^2＝４に代入すると

　　ｘ^2＋（１−√３）ｘ＋２（１−√３）^2−２＝０

　　ｘ＝（√３−１＋√２（√３−１）＝１．９４２０５

となって，近似度が劣化する．

　実際に図を描くと以下のようになって，近似的な作図にも程遠いことがわかるだろう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝