【２】区分求積法（１７世紀の積分法）

一方，弧長は，正ｎ角形の外接円の半径をｒとすると

　　Ｌn＝４ｒｓｉｎ(π/n)Σｓｉｎ(kπ/n) (k=1=n-1)

で与えられるのですが，

　　ｓｉｎα＋ｓｉｎ２α＋ｓｉｎ３α＋・・・＋ｓｉｎｎα

　＝ｓｉｎ（ｎα／２）・ｓｉｎ｛（ｎ＋１）α／２｝／ｓｉｎ（α／２）

なる関係にα←π／ｎ，ｎ←ｎ−１を代入すると

　　Σｓｉｎ(kπ/n)＝１／ｓｉｎ(π/2n)

　　Ｌn ＝４ｒｓｉｎ(π/n)Σｓｉｎ(kπ/n)

　　　 ＝４ｒｓｉｎ(π/n)／ｓｉｎ(π/2n)　→　８ｒ　　（ｎ→∞）

となります．これによりサイクロイドの弧長が外接円の直径の４倍であることが示されました．

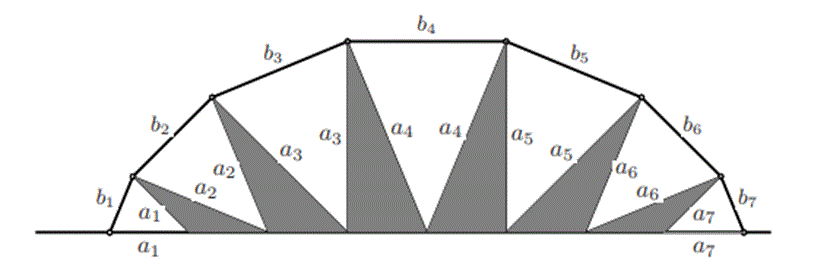
宮本次郎先生・提供

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝