π/8（デルトイド）より面積の小さい星状領域、できればπ/11より面積の小さい星状領域を構成してみたいのであるが、

実際問題としてデルトイドより面積の小さい星状領域をみつけることは簡単な問題ではない。

これからはすでに知られているシェーンベルグ集合、ボレリ集合を含む５種類の異なる星状集合を扱う。

Circular arc star shaped set (Schoenberg)

Asteroid arc star shaped set (Borrelli)

Peritrochoid arc star shaped set

Pentagram and N-cusped star shaped set

Slender N-cusped star shaped set

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

やせたN芒星でもπ/10より面積の小さい掛谷集合を構成することはできない

したがってπ/11を目指すにはシェーンベルグ集合の円弧を別の曲線に変更するしかないと思われる。

まず最初に円弧x^2+y^2=1を超円x^d+y^d=1に変更してみたところ、

d=2, ∫ dt (integrable)

d=3, ∫ (sint)^-1/3 dt (?)

d=4, ∫ (sint)^-1/2 dt (?)

が出現し、積分可能かどうかわからなかった。

次に、円弧を楕円・放物線・双曲線に変えることにしたのであるが、放物線では

∫ (cosθ)^-4 dt (integrable)

であったが、円の場合と同じ焦点と接線を持つ放物線がうまく構成できず、計算を断念した。

結局、π/11よりも小さい掛谷集合を構成することができなかった

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

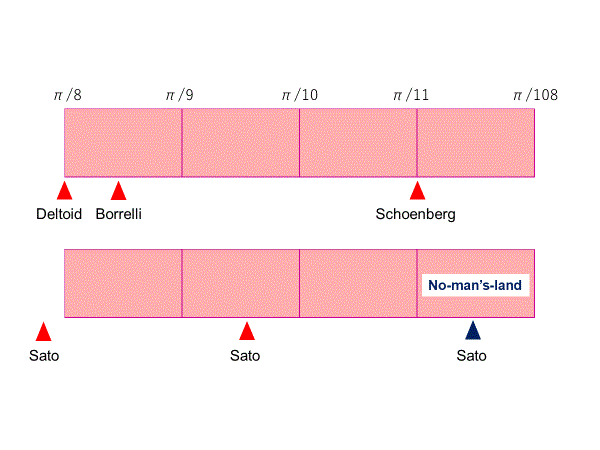
長きにわたって掛谷の問題にに取り組んできた。その粘り強さは、この問題に魅せられたことの証であるが、同時に私自身の献身的性格の証でもある。

どなたかご自分でこの計算を実行してくれる方がいるといいのですが、誰も試そうととしてくれません。

サービス精神の豊かな方々にぜひとももっと深く掘り下げてほしいと期待します。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝