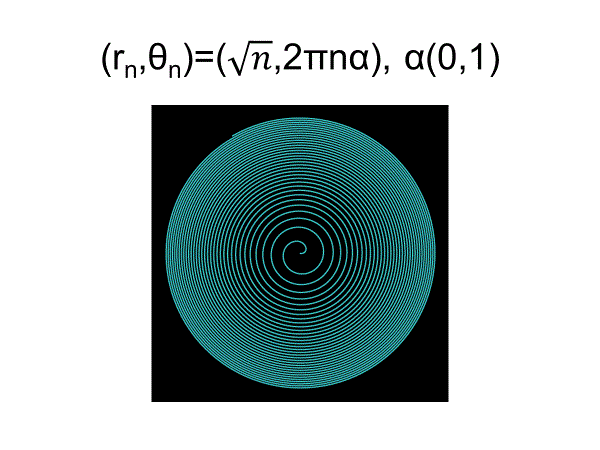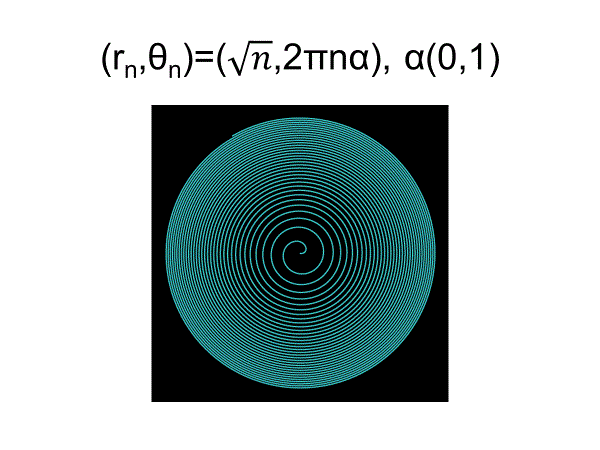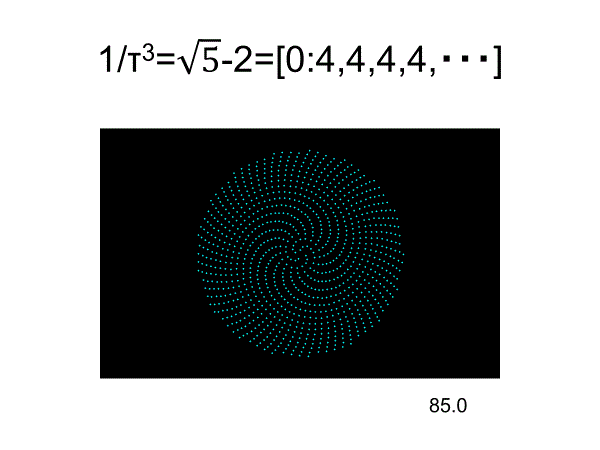フェルマーらせん上の点配置

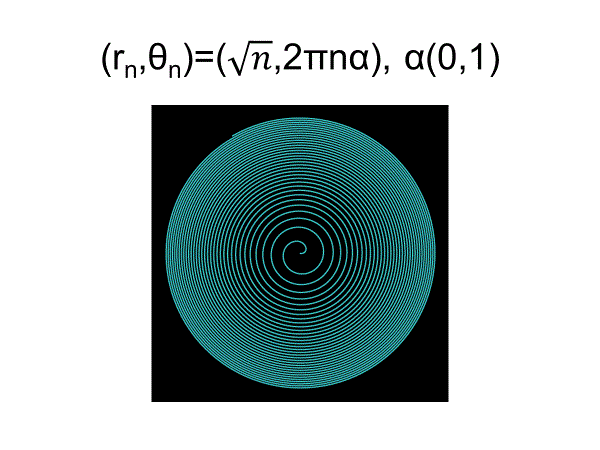
は最も効率の良い配置であって、一様分布になるためにはフェルマーらせんに限ることが証明されている(r^2=aθ, r=aθ^1/2)

したがって、これ以降は、黄金角とは360°を1:τに内分した角度(137.5 / 222.5°)であって、動径方向の分布則としてフェルマーらせんを仮定する

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

なぜフェルマーらせんなのか?という問いの対しては

黄金角以外であっても、もし無限遠において一様分布を示すならば、フェルマーらせん上の点配置になっているからである。

しかし、原点付近での振る舞いについては予測困難である。この様子を調べることにしよう。

黄金角とその補角(137.5 / 222.5°)の場合、渦巻きの方向は反対になるが本質的な点配置としては不変であろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

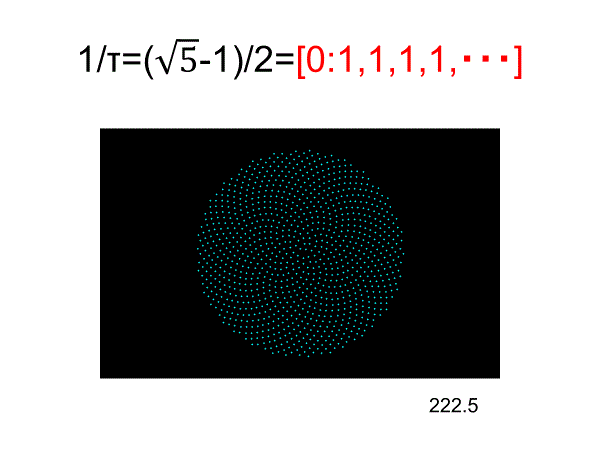
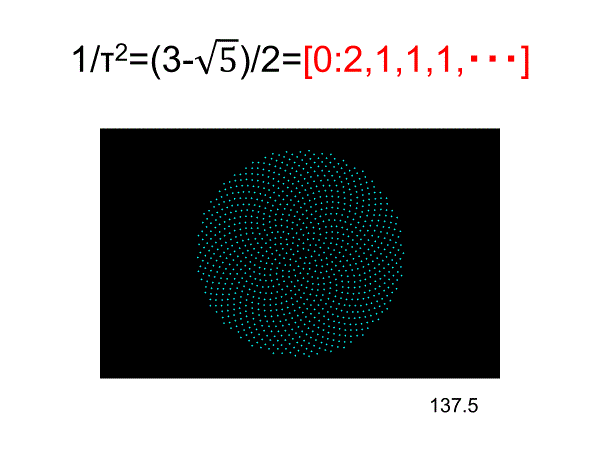
コクセターはフェルマーらせん上の点配置について考察している

コクセターによれば、フィボナッチパターンが現れるのは黄金角のときに限る　　（本当だろうか？）

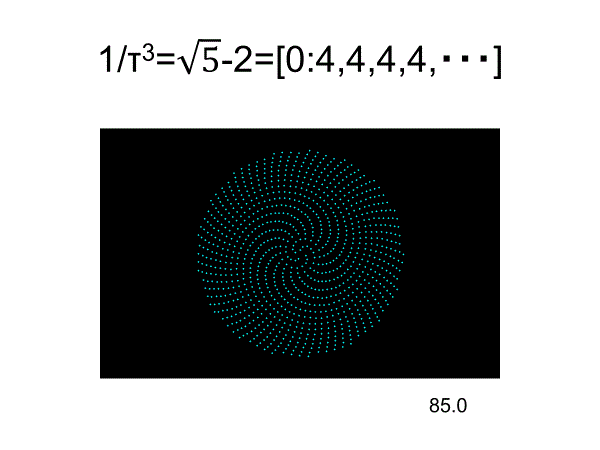
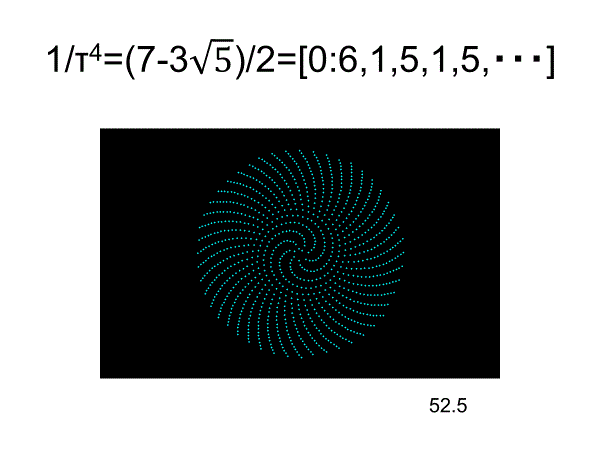
明らかにヒマワリ・パターンとは異なっていて、まるでクモヒトデのようである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝