正三角形の３つの頂点を中心にして正三角形の１辺の長さを半径とする円を描くと，正三角形に少し丸みをつけた図形ができる．これがルーローの三角形である．ルーローの三角形はどの方向の幅も最初の正三角形の１辺の長さとなる．いかなる方向に対しても等しい幅をもっている図形を「定幅図形」と呼ぶ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】直線上を転がるときの中心の軌跡

　円が直線上を回転するとき，円の中心が描く軌跡は定直線に平行な直線となります．円を正方形に置き換えてみると，頂点が回転軸となりますから，正方形の中心は中心角π／２の円弧を連ねた波型曲線を描きます．正三角形の場合，その中心（重心）は中心角２π／３の円弧をつないだ曲線になります．一般に，正ｎ角形の場合，中心角２π／ｎの円弧をつないだ曲線となるのですが，円の場合は正ｎ角形のｎ→∞のときの極限として，平行線を描くというわけです．

　また，固定した直線上を円が滑らずに転がるとき，回転円の周上の固定点のなす軌跡はサイクロイドと呼ばれます．最初の定点の位置を原点にとり，回転角を媒介変数として回転円の半径をａとすると

　　ｘ＝ａ（θ−ｓｉｎθ），ｙ＝ａ（１−ｃｏｓθ）

と書くことができます．この曲線は２変数多項式ｆ（ｘ，ｙ）＝０の形に表せませんから代数曲線でありません．

　円の内側にある固定点が描く軌跡をトロコイドというのですが，

　　ｘ＝ａθ−ｂｓｉｎθ，ｙ＝ａ−ｂｃｏｓθ　　　（ａ＞ｂ＞０）

で表されます．ｂは円の中心から固定点までの距離で，このときｙはａ−ｂ≦ｙ≦ａ＋ｂの範囲を動きます．また，サイクロイドもトロコイドもθ＝２π，ｘ＝２πａを周期とする曲線であることがわかります．

　　ｄｘ／ｄθ＝ａ−ｂｃｏｓθ＝ｙ，ｄｙ／ｄθ＝ｂｓｉｎθ

　　ｄ^2ｘ／ｄθ^2＝ｂｓｉｎθ，ｄ^2ｙ／ｄθ^2＝ｂｃｏｓθ

　　ｄ^3ｘ／ｄθ^3＝ｂｃｏｓθ，ｄ^3ｙ／ｄθ^3＝−ｂｓｉｎθ

より，

　　ｄｙ／ｄｘ＝ｂｓｉｎθ／（ａ−ｂｃｏｓθ）

　　ｄ^2ｙ／ｄｘ^2＝ｃｏｔθ

　　ｄ^3ｙ／ｄｘ^3＝−ｔａｎθ

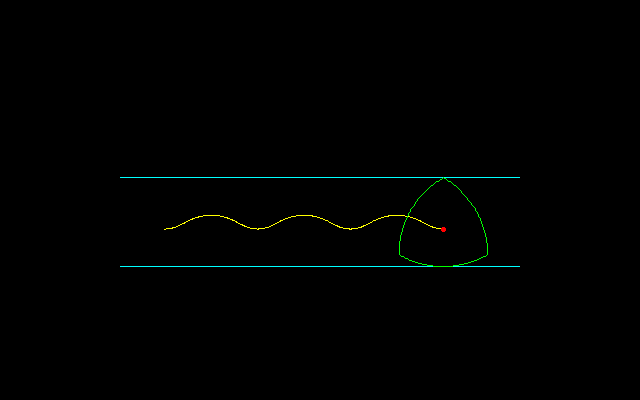
　それではルーローの三角形の中心が描く軌跡はどうなるかというと，トロコイドと中心角π／３の円弧を区分的に接続した曲線となります．その理由はルーローの三角形には３つの角があり，そこを接点として転がるときは接線同士のなす内角は２π／３ですから中心角π／３の円弧となり，一方，円周上の１点を接点として転がるときはトロコイドになるからです．

　ルーローの三角形の場合，ｂ＝ａ／√３です．また，角から中心までの距離をｃ（＝ｂ＝ａ／√３）とおき，トロコイドの最下点ｙ＝ａ−ｂの位置をｘ＝０にとると，円弧部分は

　　ｘ＝πａ／６＋ｃｓｉｎφ　　　（−π／６≦φ≦π／６）

　　ｙ＝ｃｃｏｓφ

と表すことができます．

　　ｄｘ／ｄφ＝ｃｃｏｓφ，ｄｙ／ｄφ＝−ｃｓｉｎφ

　　ｄ^2ｘ／ｄφ^2＝−ｃｓｉｎφ，ｄ^2ｙ／ｄφ^2＝−ｃｃｏｓφ

　　ｄ^3ｘ／ｄφ^3＝−ｃｃｏｓφ，ｄ^3ｙ／ｄφ^3＝ｃｓｉｎφ

より

　　ｄｙ／ｄｘ＝−ｔａｎφ

　　ｄ^2ｙ／ｄｘ^2＝ｃｏｔφ

　　ｄ^3ｙ／ｄｘ^3＝−ｔａｎφ

両者が接続する点ではφ＝−π／６ですから，円弧に関して

　　ｄｙ／ｄｘ＝−ｔａｎφ＝１／√３

　　ｄ^2ｙ／ｄｘ^2＝ｃｏｔφ＝−√３

　　ｄ^3ｙ／ｄｘ^3＝−ｔａｎφ＝１／√３

　トロコイドに関しては，円弧と連続することより

　　ｙ＝ａ−ｂｃｏｓθ＝ｃ√３／２

より，

　　ｃｏｓθ＝√３／２，ｓｉｎθ＝１／２

　　ｄｙ／ｄｘ＝ｂｓｉｎθ／（ａ−ｂｃｏｓθ）＝１／√３

　　ｄ^2ｙ／ｄｘ^2＝−ｃｏｔθ＝−√３

　　ｄ^3ｙ／ｄｘ^3＝−ｔａｎθ＝−１／√３

となって，ｙもｙ’もｙ”も一致するするように接続することがわかります．しかし，ｙ^(3)は一致していないようです．

　以上のことから，ルーローの三角形が直線上を転がるときの中心の軌跡はトロコイドの最高点ａ＋ｂを円弧の最高点ｃまで押しつぶしたような形であって，ａ−ｂ≦ｙ≦ｃ，すなわち，

　　（１−１／√３）ａ≦ｙ≦ａ／√３

の範囲を動くことになります．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

アニメができたので掲げます。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝