［１］デカルトの葉線

　　ｘ^3＋ｙ^3＝３ａｘｙ

［２］エティエンヌ・パスカル（ブレーズ・パスカルの父）の蝸牛線（リマソン）

　　（ｘ^2＋ｙ^2−ａｘ）^2＝ｂ^2（ｘ^2＋ｙ^2）

［３］グランディのバラ曲線

　　（ｘ^2＋ｙ^2）^3＝４ａｘ^2ｙ^2

［４］ベルヌーイのレムニスケート

　　（ｘ^2＋ｙ^2）^2＝２ａ^2（ｘ^2−ｙ^2）

　なぜ彼らが複雑な等式から導かれる美しい曲線を考え出したかはわからないが，バラ曲線は一般に

r=asinnθあるいはr=acosnθ

で表される。

直交座標（ｘ^2＋ｙ^2）^3＝４ａｘ^2ｙ^2を極座標に変換すれば

x=rcosθ,y=rsinθを代入してr^6=ar^4(2cosθsinθ)^2=ar^4(sin2θ)^2

r=bsin2θ となるからn=2の場合に相当することがわかる。

ｎが偶数の場合な花びらの枚数は2n枚、奇数の場合な花びらの枚数はn枚になる。

バラ曲線はスピログラフで描くことができるから、スピログラフで遊んだ思い出をお持ちのかたも少なくないだろう。

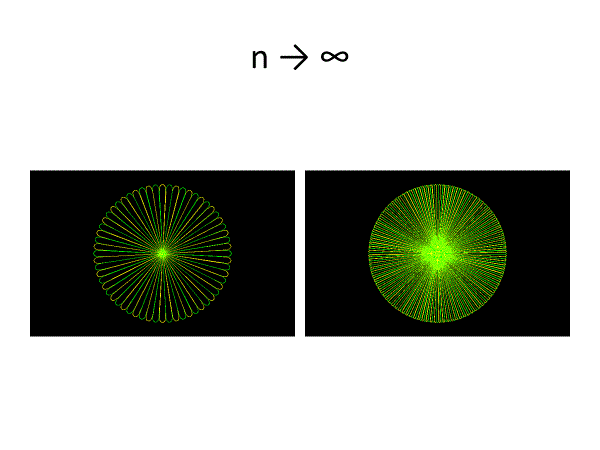
ｎが有理数n=r/sの場合、少し変わったバラ曲線を描くことができる。無理数の場合は曲線が閉じることがないため、花びらの枚数は∞となる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

レムニスケートはr^2=cos2θで表される曲線であるが、それを一般化したバラ曲線族: ｒ^(n/2)=cos(nθ/2) ではどうか？

バラ曲線と命名されているが、nが大きくなるにつれて、見た目はクローバー曲線あるいはキク曲線のほうがふさわしいかもしれない

カージオイド(n=1)は任意等分可

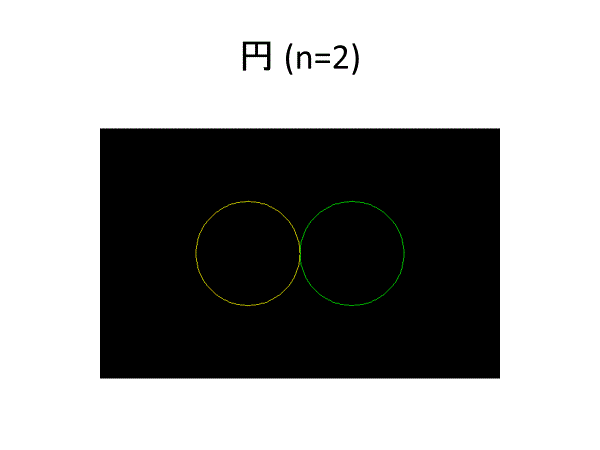
円(n=2)、レムニスケート(n=4)は2^k等分・フェルマー素数等分可

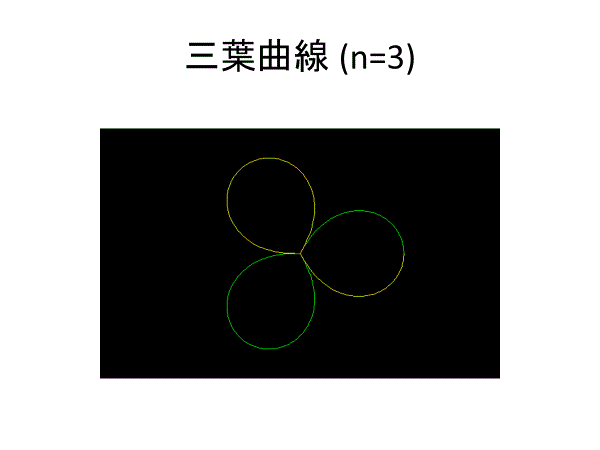
三葉曲線(n=3)、六葉曲線(n=6)は2^k等分可

五葉曲線(n=5)は等分不可である

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝