空間充填四面体、すなわち、合同な三角錐による空間充填を考える

どんな形の三角形でも平面を過不足なく敷きつめることができるのに対して、空間を隙間なく埋め尽くせる三角錐はごく稀です。サマーヴィルの等面四面体やヒルの直角錐はその稀有なる例です。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

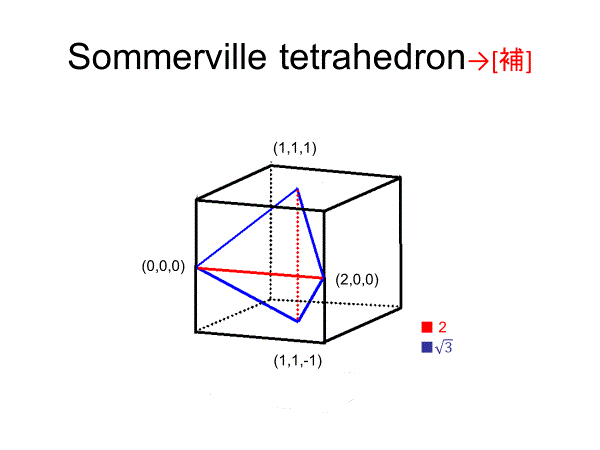
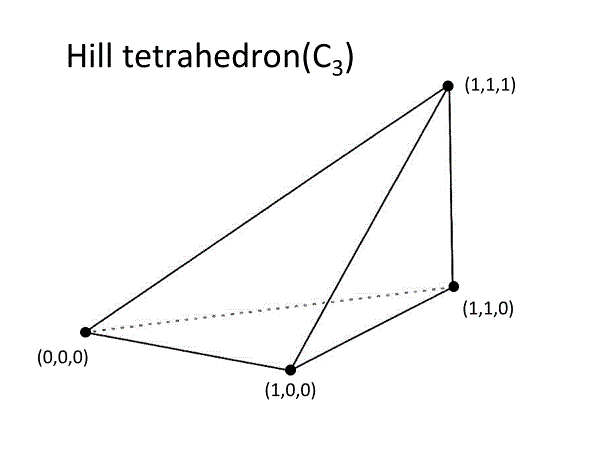
逆説的に聞こえるかもしれませんが、空間充填可能な三角錐は無数にあります。正三角柱への埋め込みが可能な三角錐に限定しても無数にあるのです。 ここでは、空間充填可能な三角錐は無数にあること、正三角柱への埋め込みが可能な三角錐は二等辺三角柱への埋め込みも可能であることを示したい。

正三角柱への埋め込みとGoldbergの基準

c2=3(b2-a2), where AB=BC=CD=a, AC=BD=b and AD=c (Goldberg).

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ここで取り上げた問題はA群無限鏡映群の問題であるから、2通りの空間充填性は3次元のみならず、すべての次元において成り立つ性質であることを申し添えておきたい。Goldbergの基準を高次元に拡張すると

3a2-3b2+c2=0 (A2 prism, Goldberg)

4a2-6b2+4c2-d2=0 (A3 prism)

5a2-10b2+10c2-5d2+e2=0 (A4 "prism")

6a2-15b2+20c2-15d2+6e2-f2=0 (A5 prism)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝