ロシアの結晶学者フェドロフは，３次元空間において，平行移動だけで決まる本質的なボロノイ領域は，たった５種類しかないという構築原理発見した（１８８５年）．この５種類のボロノイ領域とは，立方体，６角柱，菱形１２面体，長菱形１２面体，切頂８面体であって，「平行多面体」と総称される．

すなわち，平行多面体とは平行移動するだけで３次元空間を埋めつくすことのできる単独の多面体であって，２３０種類ある結晶もたった５種類のウィグナー・ザイツセルで概構成することができるのである．これら５種類の図形は５種類の正多面体（プラトン立体）ほどよく知られていないが，自然界のレゴ・ブロックと考えられる所以である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

フェドロフの平行多面体とは平行移動するだけで３次元空間を埋めつくすことのできる単独の多面体であって，平行辺（したがって平行四辺形面，平行六辺形面に限られる），平行面から構成されている多面体である．フェドロフの平行多面体には立方体，６角柱，菱形１２面体，長菱形１２面体，切頂８面体の５種類しかないことが証明されている（１８８５年）．

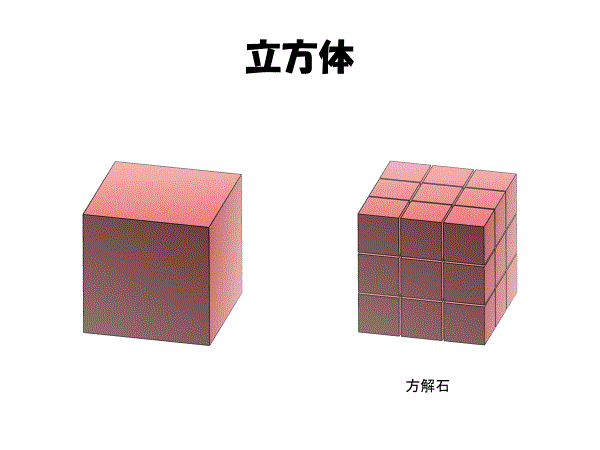
立方体は単独で空間全体を格子状に埋めつくすことができる．単純立方格子状配置，すなわち角砂糖の箱の封を切ったときに見えるパターンについてはこれ以上説明するまでもないだろう．立方体以外の単一多面体による空間充填体としては，菱形十二面体や切頂八面体がよく知られている．両者はしばしば対比され，どちらも単独で空間充填可能な立体図形であるが，菱形十二面体が面心立方格子のボロノイ図であるのに対して，切頂八面体は体心立方格子のボロノイ図となっている．

平行多面体は結晶（金属結晶や鉱物結晶）でよくみられる構造である．菱形１２面体はザクロ石（ガーネット）にもみられる．立方体は単純立方格子のボロノイ領域で，平行六面体は方解石にみられる．六角柱はコランダム（ルビー・サファイア），歯のエナメル質などにみられるが，長菱形１２面体はあまりみられないから平行多面体の異端児である．

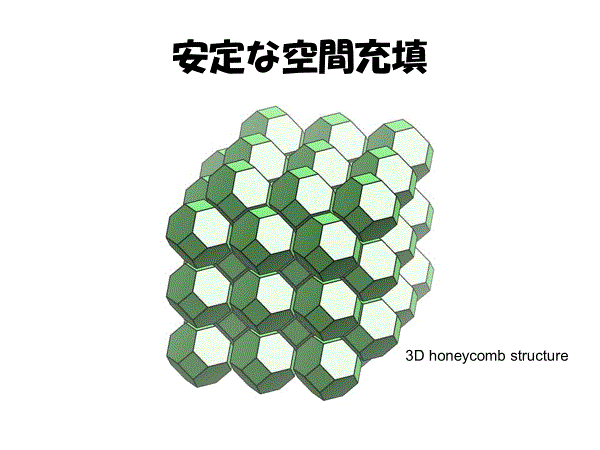
これら５種類の図形は３次元格子の幾何学的分類であり，５種類の正多面体（プラトン立体）ほどよく知られていないが，少なくとも同じ程度に重要であるし，結晶学の観点からすると平行多面体は正多面体以上に重要である。とりわけ原始的平行多面体である切頂八面体による空間充填は・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝