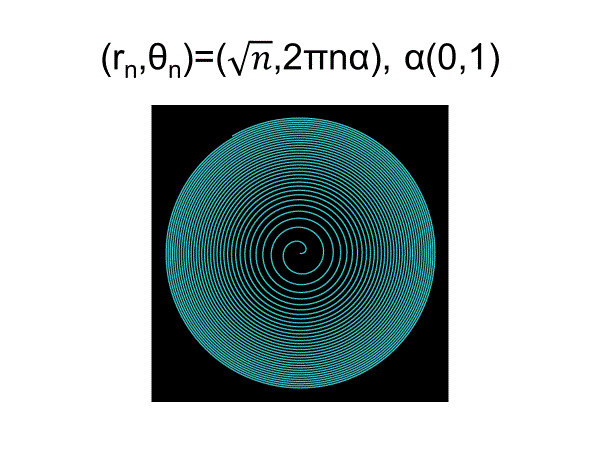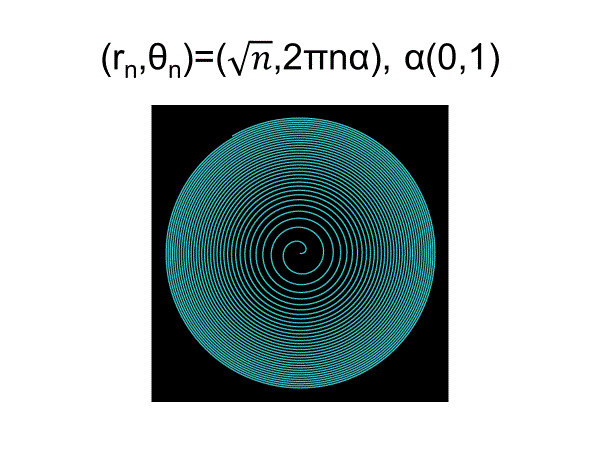フェルマーらせんｒ^2＝ａθの幅は中心から離れるほど小さくなる．フェルマーらせんは形式的には放物線ｙ^2＝ａｘと似ていることから放物らせんとも呼ばれる．

フェルマーらせん上の円配置についてみてみよう

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ヒマワリのらせん

植物構造に現れるフィボナッチ数は、パイナップルやマツカサ、ヒマワリなどいろいろなところで見られる。通常，ヒマワリの花芯では左巻き21重、右巻き33重、左巻き55重らせんなど時計回りと反時計回り２方向の互いに交わる多重らせんが現れる。これがFibonacciらせんと呼ばれる所以である。多数の対数らせんが最も稠密に絡み合って魅惑的なパターンの花芯となるのである．

黄金角とは360°を1:φに内分した角度(137.5°,222.5°)をさす。動径方向の分布則としてフェルマーらせんを仮定する。フェルマーらせんと黄金角が結びつくと、一様な点分布が形成される。逆に一様分布になるためにはフェルマーらせんに限ることが知られている

コクセターによれば、フィボナッチパターンが現れるのは黄金角のときである 。植物の構造に、なぜこの特別な角度が現れるのかという謎を解くカギはフェルマーらせんにあったのである。フェルマーらせんでは最も効率の良い配置が得られるのである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
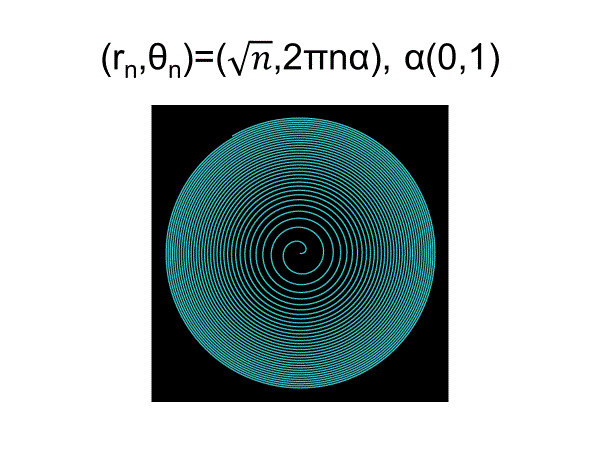