飛んで火に入る夏の虫

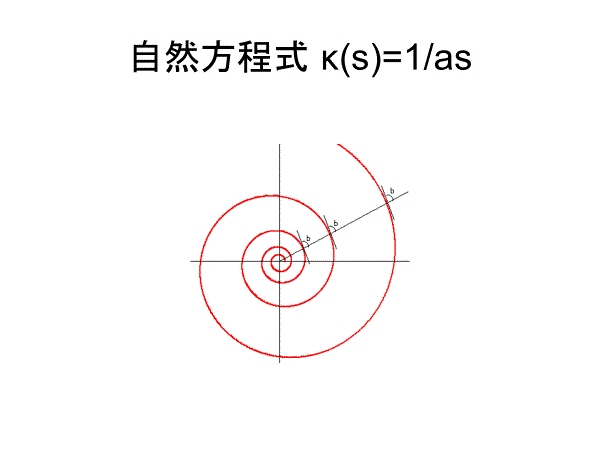
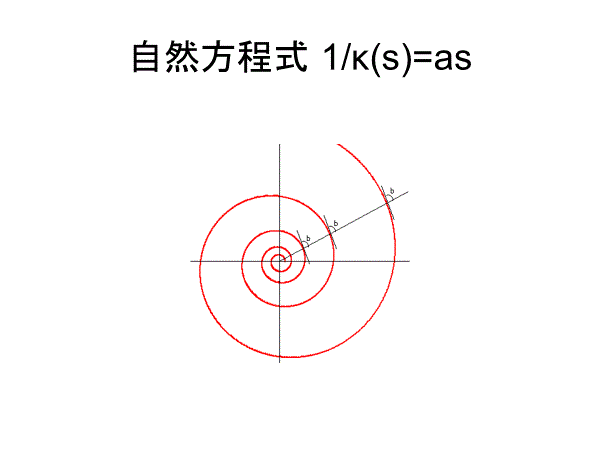
対数らせんには、動径をいつも一定の角度で横切るという特徴があり，等角らせんとも呼ばれています． 昆虫には太陽光線に対して一定の角度を維持しながら飛ぶという習性があり，（太陽光線は平行光線とみなせるので日中は問題ないが）夏の夜，街灯や集蛾灯の回りをぐるぐる飛び回る虫の飛跡は対数らせんとなります

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

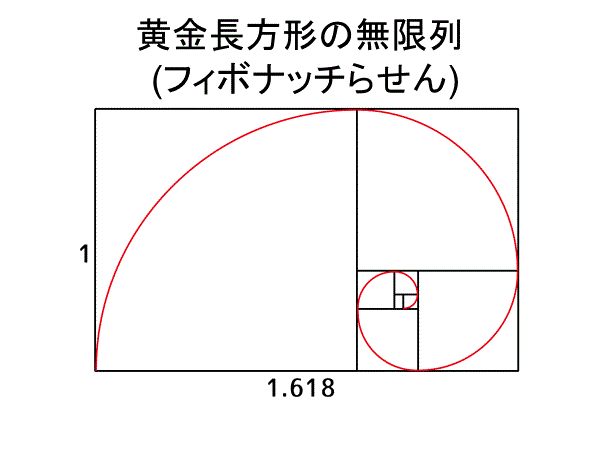
渦巻状に並ぶ黄金長方形列タイル

黄金長方形の辺を1辺とする正方形を描くと，さらに大きな黄金長方形ができる．正方形内に１／４円弧を描く．この手順は無限に繰り返すことができて，黄金らせんに近いらせんを作ることができる．これはフィボナッチ数を視覚的に表す有名な方法である

貝のなかには黄金長方形の無限列よりなる対数らせん構造をもったものがある。対数らせんは，アルキメデスのらせんとは違って，一定の割合で間隔が開いていく．実際にみられる黄金らせんの例として，オウムガイの殻がある．殻の中で成長するにつれて殻も伸びていき，成長しても浮力が一定に保たれるのである．

黄金らせんは成長してもその形であって，ヤコブ・ベルヌーイはこのらせんがとても気に入っていた．そして，自分の墓碑銘に黄金らせんを刻むように頼んだという． しかし，石工は黄金らせん（ベルヌーイのらせん,ｒ＝ａ^θ）を間違って，アルキメデスのらせんｒ＝ａθを刻んでしまったというこぼれ話が残されている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝