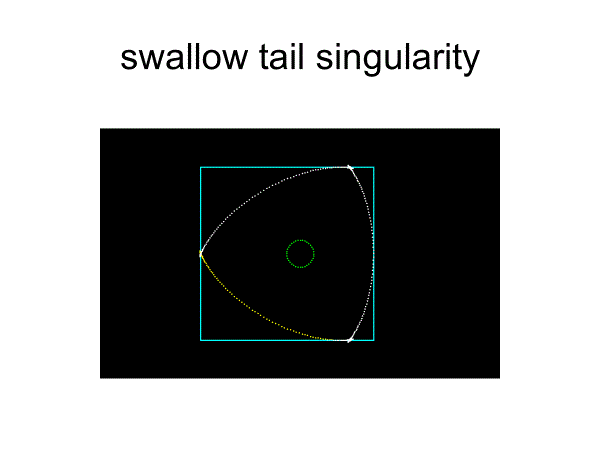
ルーローの三角形は正方形の内転形ではあるが、その中心軌道が円ではなく、工学応用上の欠点があった。

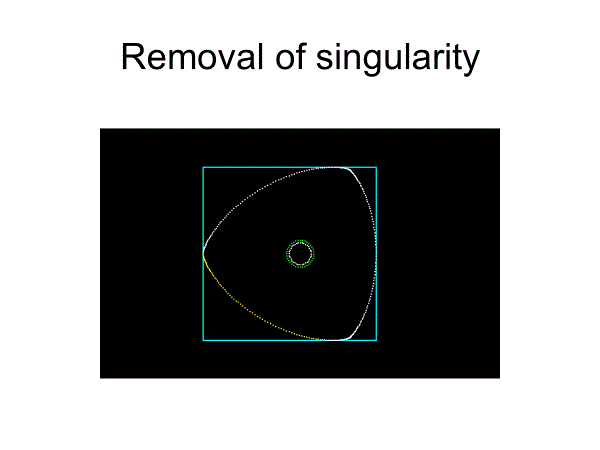
中心軌道を円にするため、ほぼ正方形のペリトロコイド曲線に代替した。これは近似的な解を与えるものではあるが、精確に正方形に沿って動くものではない。

ところで、・・・フーリエ級数と呼ばれる関数展開は， １９世紀初頭，フランスの数学者・物理学者フーリエが熱伝導に関する著作の中で，鉄の輪を熱したときの温度分布を解析するなど熱伝導の考察から誕生し，任意の周期関数ｙ＝ｆ（ｘ）がサインとコサインの項の和，すなわち，単振動（調和振動）の和に分解されることを証明したことに始まります．

フーリエ級数は波動や振動現象の解明をはじめ多くの応用分野をもっています．正五角形の内転形となる円弧四角形は存在しないことが証明されている。しかし、フルヴィッツのフーリエ級数論は、正五角形、正六角形、・・・にも応用できる。

x=(n-2)cos(nt)+ncos(n-2)t-2n(n-2)sint

y=-(n-2)sin(nt)+nsin(n-2)t -2n(n-2)cost

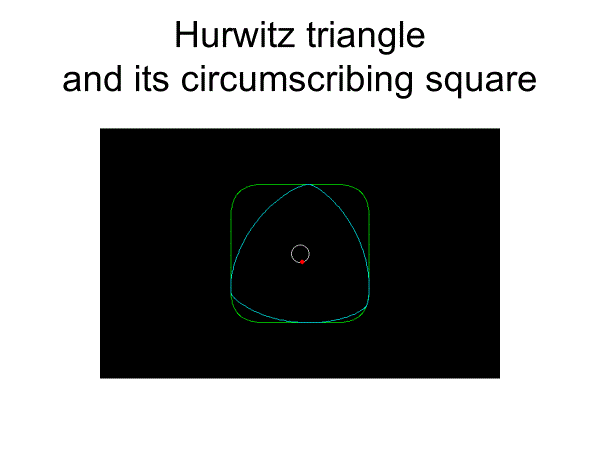
円弧偶数角形は精確な奇数角形の内転形になりえないが、非円弧内転形を構成することは可能である。ここではフルヴィッツのフーリエ級数論の応用として、中心軌道が円で、精確に正三角形・正方形・正五角形に沿って動く機構を紹介する。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝