定幅図形は偶数角形の内転形になることはわかったが、奇数角形の内転形になるのはどのようなものなのだろうか？

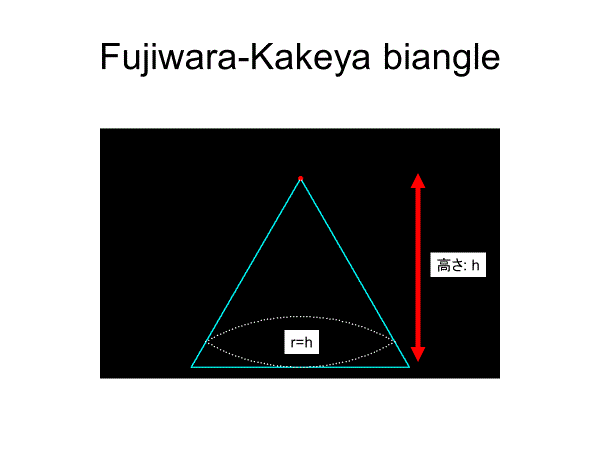
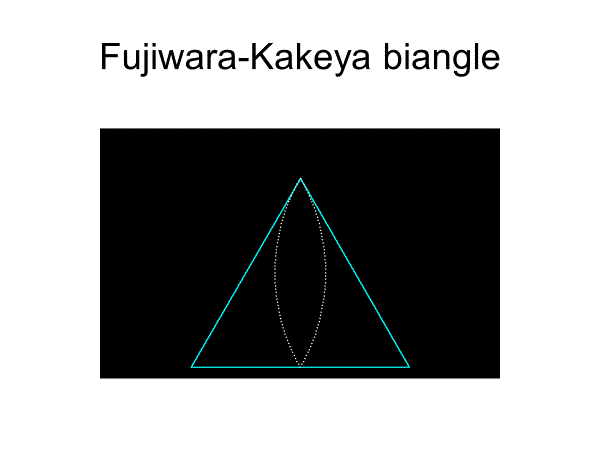
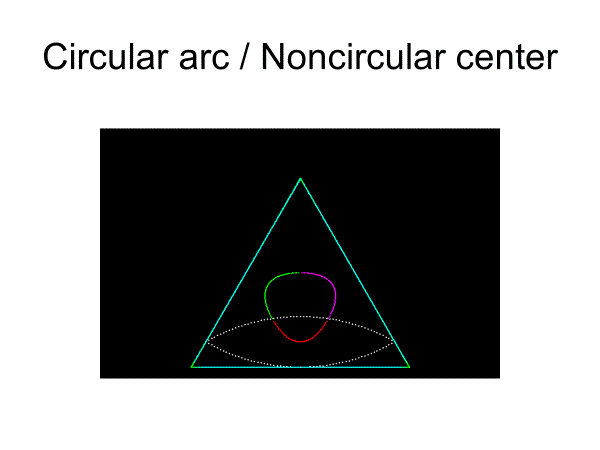
実際に、正３角形に内接しながら回転することできる凸閉曲線は円以外にも存在します．このような図形の一例が，正三角形の中線を一辺とする正三角形の頂点を中心として，中線の長さを半径とする２個の円弧からなる曲線（藤原・掛谷の２角形）です。この図形を応用すれば正３角形の穴をあけるドリルを作ることが可能になります．

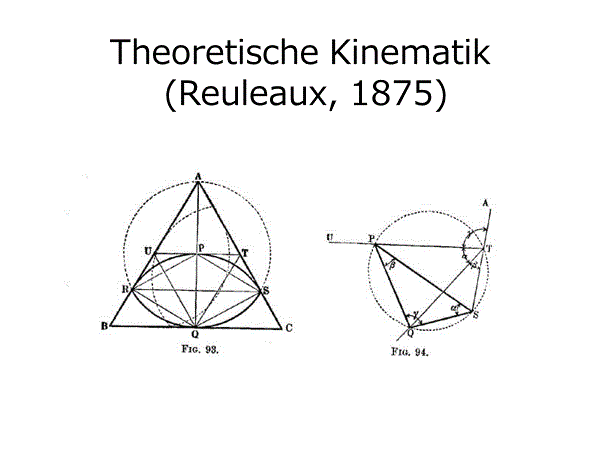
その中心軌道は楕円を区分的に連結した曲線となる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

正三角形の内転形も無数にあるが、代表的なものは藤原・掛谷の２角形以外に

ルーローの二角形（その中心軌道は楕円を区分的に連結した曲線）

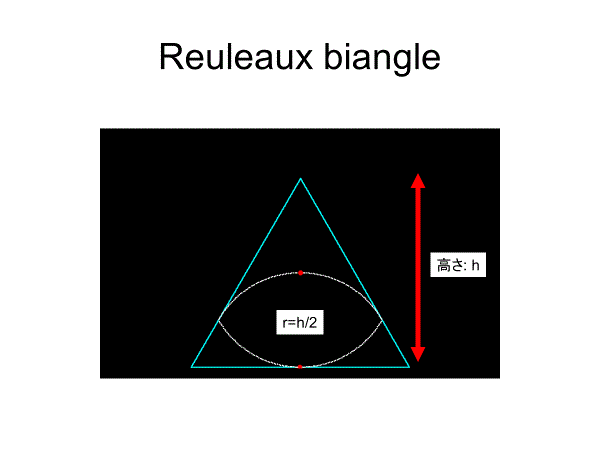
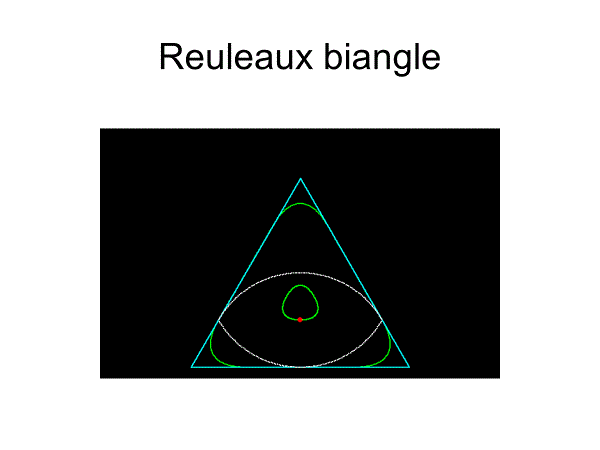
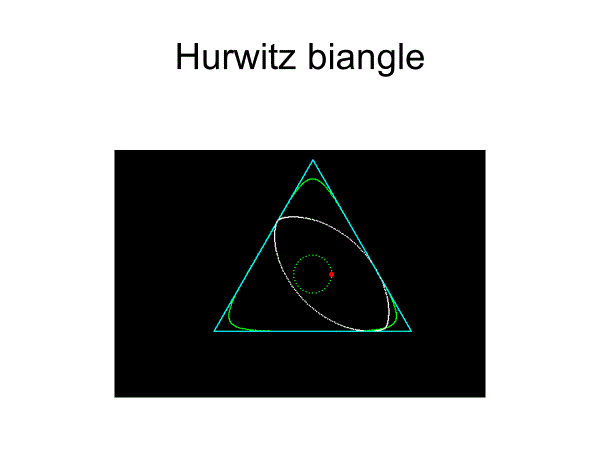
や

フルヴィッツの二角形があげられる。フルヴィッツの二角形の中心軌道は円になる。

内転形定理（藤原の定理）

1.すべての内転形（凸多角形の各辺に接しながら、その中で１回転できる卵形線）の周長は等しい。

2.正三角形の内転形で面積最小のものは、藤原・掛谷の二角形である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝