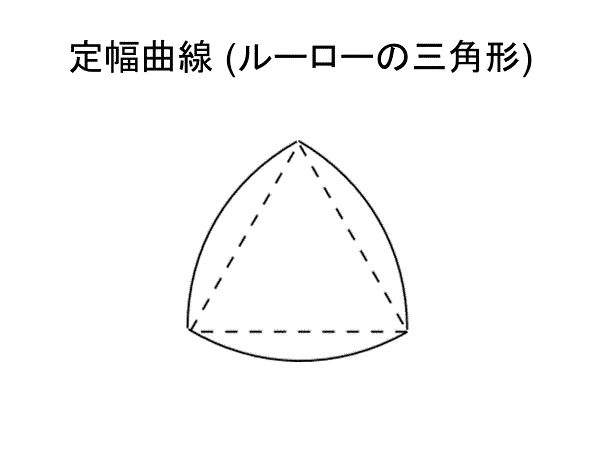
正三角形の３つの頂点を中心にして正三角形の１辺の長さを半径とする円を描くと，正三角形に少し丸みをつけた図形ができる．これがルーローの三角形である．ルーローの三角形はどの方向の幅も最初の正三角形の１辺の長さとなる．

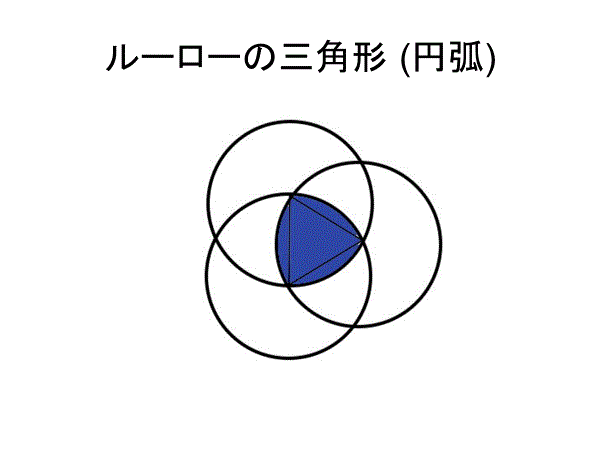
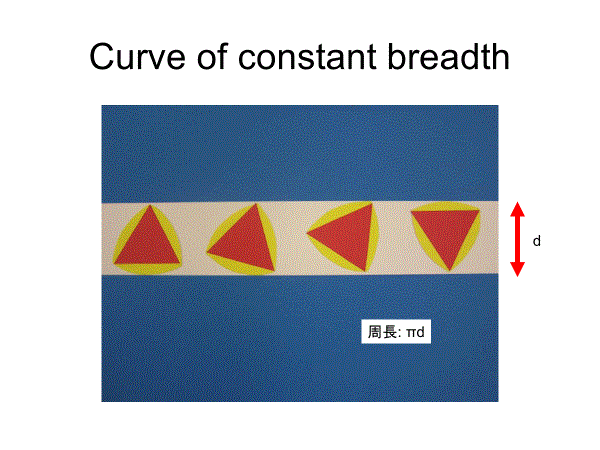
定幅図形の中で最大の面積をもつものは円であり，最小の面積をもつものはルーローの三角形です（ルベーグ１９１４年）．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ルーローの三角形は「定幅図形」であるから，どんな向きにおいても同じ長さを１辺とする正方形のなかにピッタリ収まる．

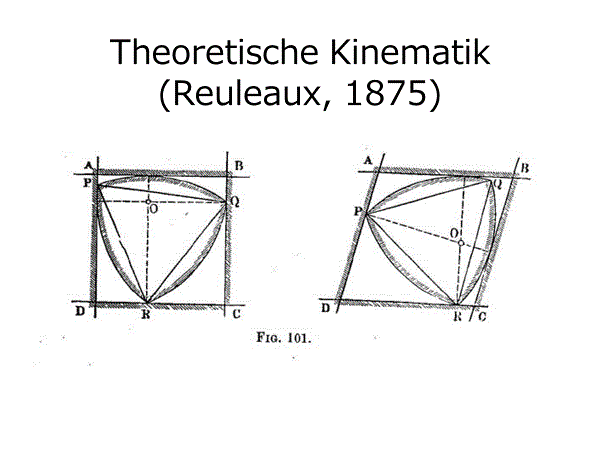
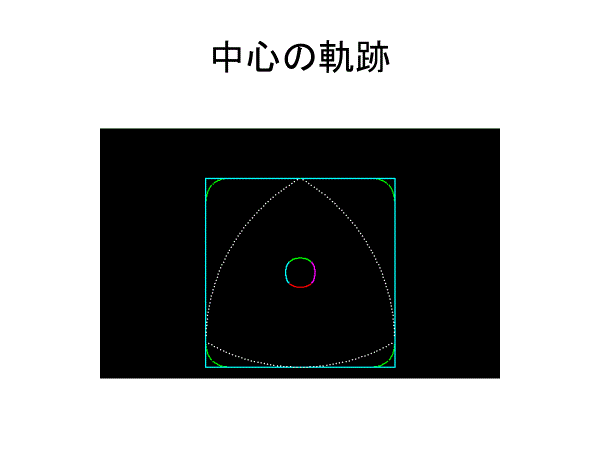
収まるのみならず正方形の中で回転することができる。正方形の４辺に接しながら回転できる図形が「内転形」である。

そこでドリルの刃をルーローの三角形にすると四角い穴もあけられることになる．

このとき、ルーローの三角形の中心は楕円をつないだ曲線を描く

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝