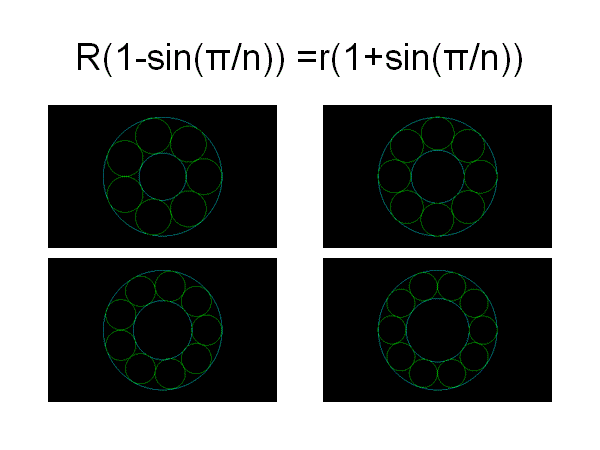曜星と呼ばれる紋様では、

外側の大円の半径をR

内側の小円の半径をr

両者に接する円の個数をｎとおくと

R(1-sin(π/n)) =r(1+sin(π/n))

が成り立つ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

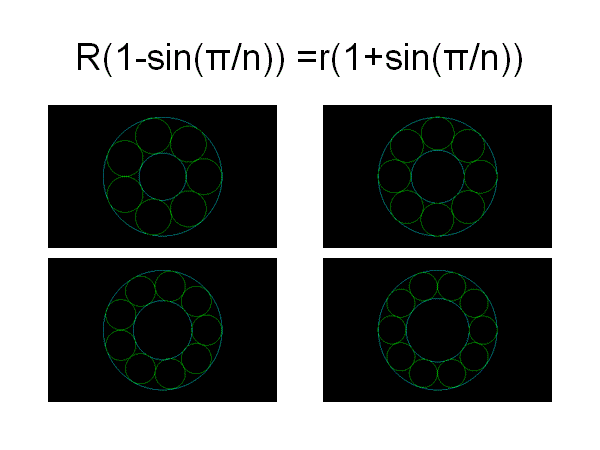
R=1, n=6のとき

(1-1/2) =r(1+1/2)、ｒ＝1/3

となって、両者に接する円の半径は

(R-r)/2=1/3=r

となり、内側の小円の大きさと等しくなる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

R=1, n=7のとき

(1-sin180/7) =r(1+sin180/7)、ｒ＝(1-sin180/7)/(1+sin180/7)

となって、両者に接する円の半径は

(R-r)/2=(sin180/7)/(1+sin180/7)＜ｒ

となると計算される。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

七曜星の問題を別の方法で解いてみたい。

外側の円に接する6個の小さな円はすべて同じ大きさなので、それを見込む角の半分は180/6に等しい。

小さい円の半径を1とすれば、大きい円の半径は

1+1/sin(180/6)＝3

となる。

したがって、

大きい円の半径を1とすれば、小さい円の半径は

1/{1+1/sin(180/6)}〜1/3

となる。

円環をなす小円と同じ大きさの円を中央に置けば、両者は接する

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝