これまで，正四面体４８個（１単位６個）の偽環に引き続き，中川宏さんによる正四面体４０個（１単位８個）の偽環を計算したが，今回のコラムで取り上げるのは正四面体８４個（１単位７個）の偽環である．・・・再び3の倍数となった

40=2^3・5

84=2^2・3・7

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

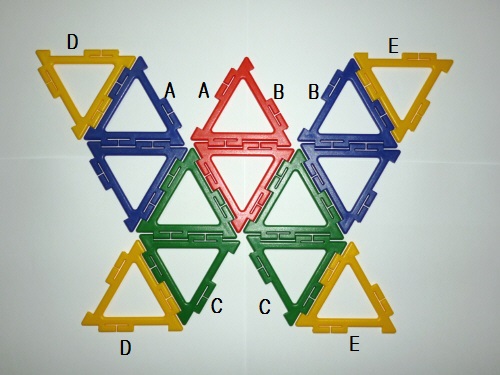
　中川八十四環の場合，頂点数：８７となるが，八十四環の座標を数値計算し，最初の３個の頂点と最後の３個（８５−８７）の頂点３個の座標を比較することにした．

　　Ａ（１／√２，０，−１）

　　Ｄ（１／√２，０，１）

　　Ｃ（−１／√２，１，０）

　　Ｂ（−１／√２，−１，０）

を初期値として，次の頂点座標を計算をするのであるが，この数値計算の欠点は，誤差が累積を避けられないことである．

　一方，利点は，ポリドロン模型では重力の影響でねじれ角が狂ってくるが，数値計算では無重力状態で計算できることである．

　辺の長さ２に対して，３点間の距離は

　　１．１７３７８，０．８５５８７８，１．１００４１

であった．ｘ方向にわずかに隙間のできる偽環になることがわかった．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝