ポンスレーの不定命題

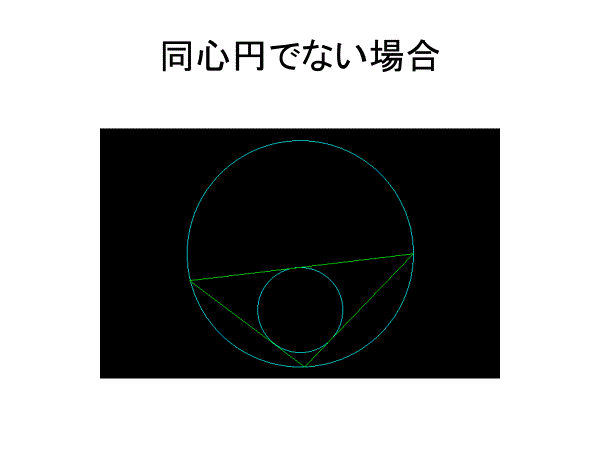
小円を大円の内部におく．大円上の点Ｐ0から小円へ接線を引き，大円と交わる点をＰ1とする．Ｐ1から再び小円へ接線を引き，大円と交わる点をＰ2とする．この２つの円の中間に次々に接する接線列を作る．たいていの場合，最後の交点は最初の点Ｐ0と重ならない．しかしときとして完全に重なる場合がある．このとき，最初の点Ｐ0をどこに選ぼうとも完全な多角形環をなす．

シュタイナーの定理とポンスレーの定理、２つの定理に共通する特徴は２つの円が同心円ならば自明であるということである．円鎖が閉じるか、接線多角形が閉じるかの違いだけで、内容的には類似した定理に感じられる。しかし、シュタイナーの定理はメビウス変換により同心円の場合に帰着させて証明できるのに対して，ポンスレーの定理ではそれができない．その意味で 2つの定理は似て非なるものである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

同心円でない場合も、最後の点が最初の点とうまく一致するならば、最初の点をどこから始めたとしても接線多角形は閉じる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝