シュタイナーの不定命題

小円を大円の内部におき，この２つの円の中間に次々に接する円列を作る．たいていの場合，最後の円は重なってしまい，この円列は互いに接する円環をなさない．しかしときとして完全な円環をなす場合がある．このとき，最初の円をどこに選ぼうとも完全な円環をなす．

シュタイナーの定理において、n→∞の場合がアルキメデスのアルベロスである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

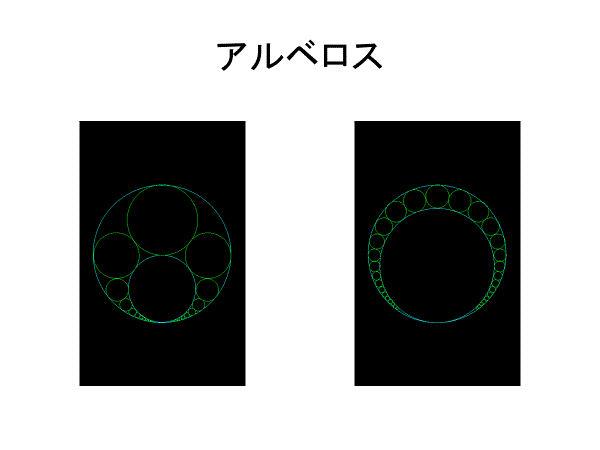
このようにｎ同心円でない場合、

外接円の半径:R

内接円の半径:r

外接円と内接円の中心間距離:d

s=(1-sin(π/n))/(1+sin(π/n))

とおくと

2次同次式: d^2=R^2-Rr(s+1/s)+r^2

=(R-rs)(R-r/s)が成り立つ

同心円の場合、r/R=s, R(1-sin(π/n)) =r(1+sin(π/n))でr/Rは最大となる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝