ペリトロコイド曲線

x=e・cos(n-1)t+R・cost

y=e・sin(n-1)t+R・sint

は古代ギリシャ時代から天体の運動模型として使われてきた曲線である。

パラメータをうまく選ぶと以下のような水色の曲線となる。円運動の合成だから、直線は含まず、近似的な正方形となるのである

以下の写真は個の応用：四角形の穴をあけるドリルとアルミにあいた四角い穴である

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（その２４）を補足

フルヴィッツ曲線では直線を偏心回転させたが、ペリトロコイドは点を偏心回転させたものとみなすことができる

x=R, y=0 (point)

Eccentric rotation:

[X]=[cos(t),-sin(t)][x]+[e・cos(n-2)t]

[Y]=[sin(t), cos(t)][y]+[e・sin(n-2)t]

X=e・cos(n-1)t+R・cost

Y=e・sin(n-1)t+R・sint

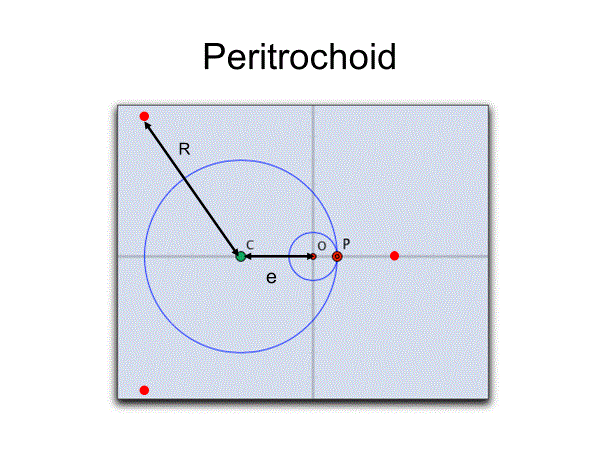
x=e・cos(n-1)t+R・cost (peritrochoid)　　

y=e・sin(n-1)t+R・sint

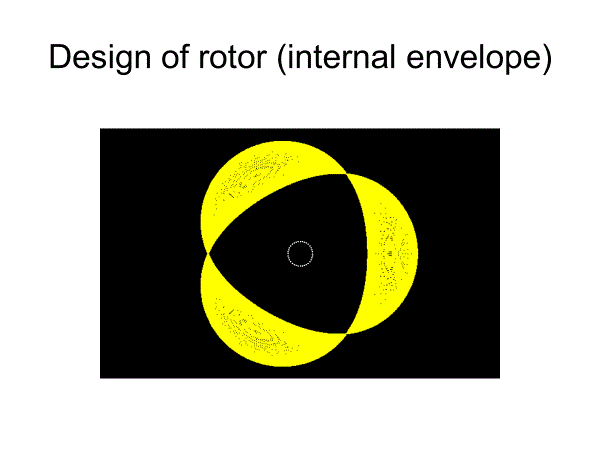
を偏心回転させて内包絡線を求めたものがローターの形となる

Eccentric rotation:

[X]=[cos(s),sin(s)][x]+[e・cos(n-2)s]

[Y]=[-sin(s),cos(s)][y]+[e・sin(n-2)s]

X=e・cos{(n-1)t-s}+R・cos(t-s)+e・cos(n-2)s

Y=e・sin{(n-1)t-s}+R・sin(t-s)+e・sin(n-2)s

(∂X/∂t)(∂Y/∂s)=(∂Y/∂t)(∂X/∂s) ⇒ s=f(t)

s=t-2/(n-1)・θ-2kπ/(n-1)

θ=arctan{R・sin(n-2)t/(R・cos(n-2)t+e・(n-1))}

t=[φ/(n-2), (2π-φ)/(n-2)]

φ=arccos{-e・(n-1)/R}, K=R/e>(n-1)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝