100年前の仙台（東北大学）発の数学問題をとりあげたい

[1]藤原松三郎の問題

　　正三角形に内接しながら回転することができる円以外の図形は何か（東北大学理科報告、１９１５年）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

私の知る限り、藤原の問題の解は3つある。（円は除く）

[1]ルーローの二角形

[2]藤原・掛谷の二角形

[3]フルヴィッツの二角形

[1],[2]は円弧二角形であるが[3]はそうではない

定理

1. There are infinitely many kinds of in-revolvable curves of N-gon. Perimeters of them are equal (Fujiwara)

2. Among in-revolvable curves of equilateral triangle, Fujiwara-Kakeya biangle has smallest area; (2π-3√3)h2/6 (Fujiwara) (Circle; πh2/9 Reuleaux; (4π-3√3)h2/24)　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

[3]フルヴィッツの二角形

円弧二角形ではないが 、中心軌道が円のため、工学応用が期待できる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

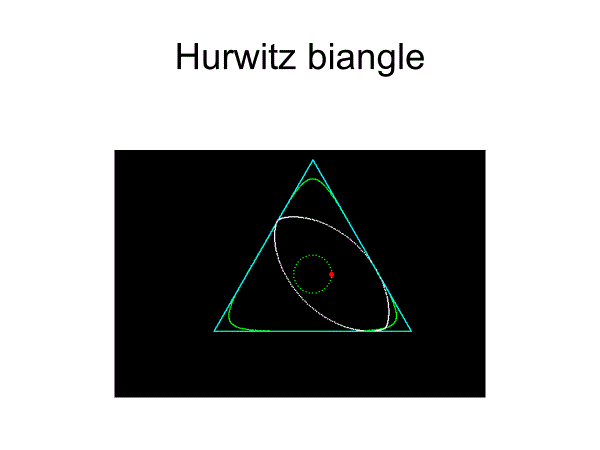
フルヴィッツ曲線は

x=(n-2)cos(nt)+ncos(n-2)t-2n(n-2)sint

y=-(n-2)sin(nt)+nsin(n-2)t -2n(n-2)cost

で与えられる。ｎ＝3とおいた場合がフルヴィッツの二角形である。

Hurwitz A.: Sur quelques applications geometriques des series de Fourier (1902)

は等周問題をフーリエ級数を用いて解いた有名な論文であるが、接線極座標が用いられているため、現代人にはわかりにくいだろう

それを参考にして、デカルト座標に変換したものが

x=(n-2)cos(nt)+ncos(n-2)t-2n(n-2)sint

y=-(n-2)sin(nt)+nsin(n-2)t -2n(n-2)cost

である。

n=3と置くと

x=2(cost)^3 - 3sint

y=2(sint)^3 - 3cost

となるが、これがアステロイドの平行曲線になっていることに留意してほしい。

n=4とおくとデルトイドの平行曲線が得られる。

これらの包絡線を求めると一部分が直線になるのである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

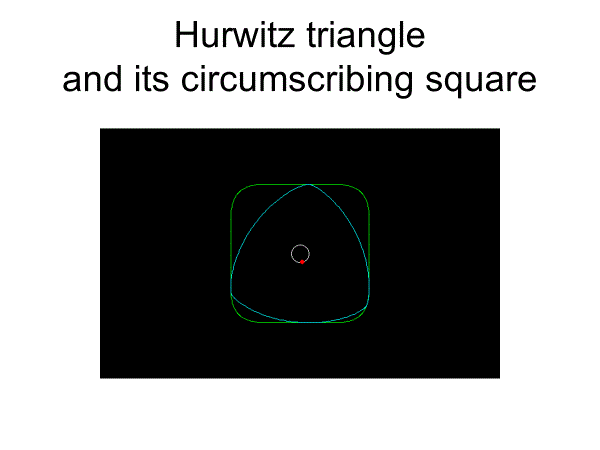
（その２２）を補足

ローターの設計ではまずその外枠となる直線を偏心回転させる

x=s, y=-R (line segment)

Eccentric rotation:

[X]=[cos(t),sin(t)][x]+[e・cos(n-2)t]

[Y]=[-sin(t),cos(t)][y]+[e・sin(n-2)t]

X=s・cos(t)-R・sin(t)+e・cos(n-2)t

Y=-s・sin(t)-R・cos(t)+e・sin(n-2)t

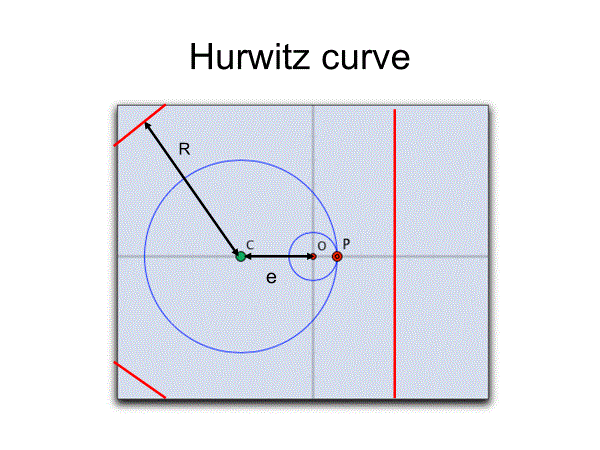
これにより特異点を生ずるが、それを除去する

(∂X/∂t)(∂Y/∂s)=(∂Y/∂t)(∂X/∂s) ⇒ s=f(t)

x=(n-2)e・cos(nt)+ne・cos(n-2)t-2R・sint

y=-(n-2)e・sin(nt)+ne・sin(n-2)t-2R・cost

x’y”-x”y’→ K=R/e≧n(n-2) (singularity)

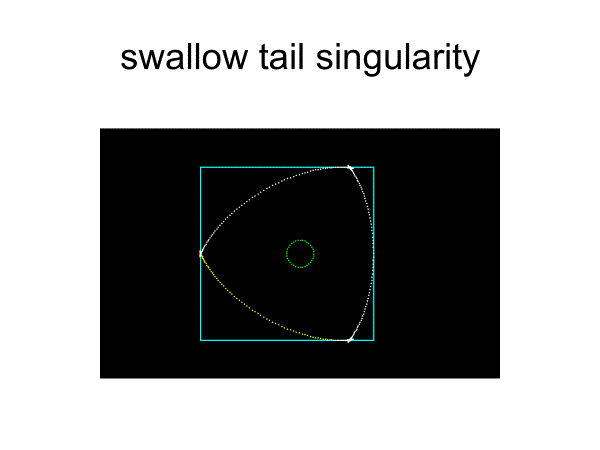
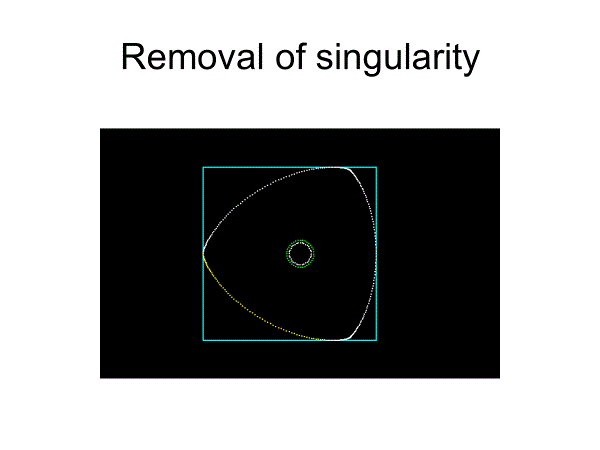
こうして得られる曲線がフルヴィッツ曲線である

x=(n-2)cos(nt)+ncos(n-2)t-2n(n-2)sint

y=-(n-2)sin(nt)+nsin(n-2)t -2n(n-2)cost

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝