100年前の仙台（東北大学）発の数学問題をとりあげたい

[1]藤原松三郎の問題

　　正三角形に内接しながら回転することができる円以外の図形は何か（東北大学理科報告、１９１５年）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

私の知る限り、藤原の問題の解は3つある。（円は除く）

[1]ルーローの二角形

[2]藤原・掛谷の二角形

[3]フルヴィッツの二角形

[1],[2]は円弧二角形であるが[3]はそうではない

定理

1. There are infinitely many kinds of in-revolvable curves of N-gon. Perimeters of them are equal (Fujiwara)

2. Among in-revolvable curves of equilateral triangle, Fujiwara-Kakeya biangle has smallest area; (2π-3√3)h2/6 (Fujiwara) (Circle; πh2/9 Reuleaux; (4π-3√3)h2/24)　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

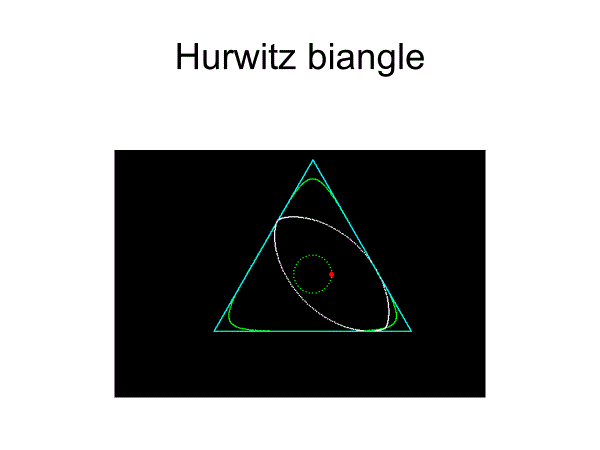
[3]フルヴィッツの二角形

円弧二角形ではないが 、中心軌道が円のため、工学応用が期待できる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

（その２０）を補足

N角形の内転形は無数にあり、3角形の場合もそうである。

3角形の内転形はアステロイドの平行曲線であるが、その１例が

x=2(cost)^3 - 3sint

y=2(sint)^3 - 3cost

である。一般に、

x=w1(cost)^3 +w2sint

y=w1(sint)^3 +w2cost

と書くことができるが、|w1/ｗ2|が大きいときはアステロイド、小さいときは円に近づく。

これらはすべて正三角形の内転形ある

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝