100年前の仙台（東北大学）発の数学問題をとりあげたい

[1]藤原松三郎の問題

　　正三角形に内接しながら回転することができる円以外の図形は何か（東北大学理科報告、１９１５年）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

私の知る限り、藤原の問題の解は3つある。（円は除く）

[1]ルーローの二角形

[2]藤原・掛谷の二角形

[3]フルヴィッツの二角形

[1],[2]は円弧二角形であるが[3]はそうではない

定理

1. There are infinitely many kinds of in-revolvable curves of N-gon. Perimeters of them are equal (Fujiwara)

2. Among in-revolvable curves of equilateral triangle, Fujiwara-Kakeya biangle has smallest area; (2π-3√3)h2/6 (Fujiwara) (Circle; πh2/9 Reuleaux; (4π-3√3)h2/24)　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

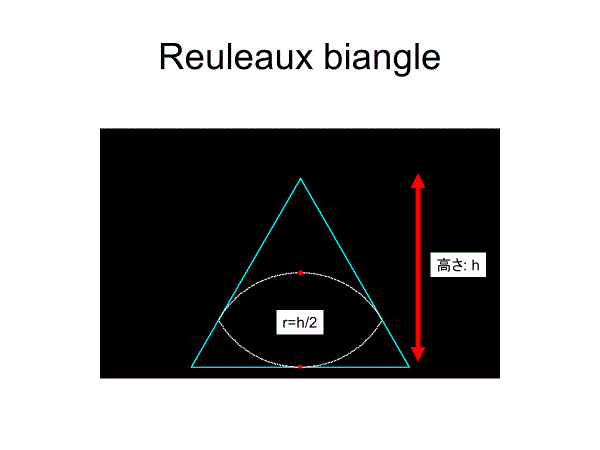
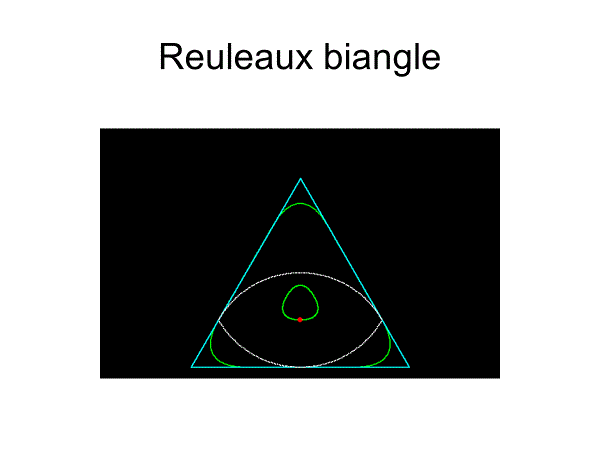
[1]ルーローの二角形

円弧二角形で、円弧の半径は正三角形の高さをｈとすると、h/2である。

レンズ型の頂角は120°である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝