100年前の仙台（東北大学）発の数学問題をとりあげたい

[1]藤原松三郎の問題

　　正三角形に内接しながら回転することができる円以外の図形は何か（東北大学理科報告、１９１５年）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

円はどの方向から測っても幅が一定の定幅曲線である。しかし、定幅曲線は円だけではなく、ルーローの三角形もその１例である。

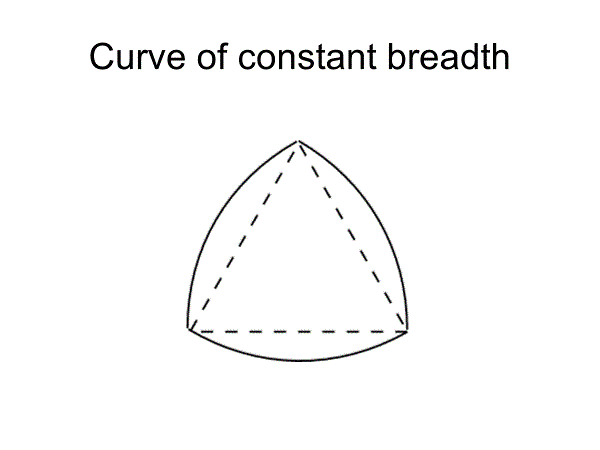
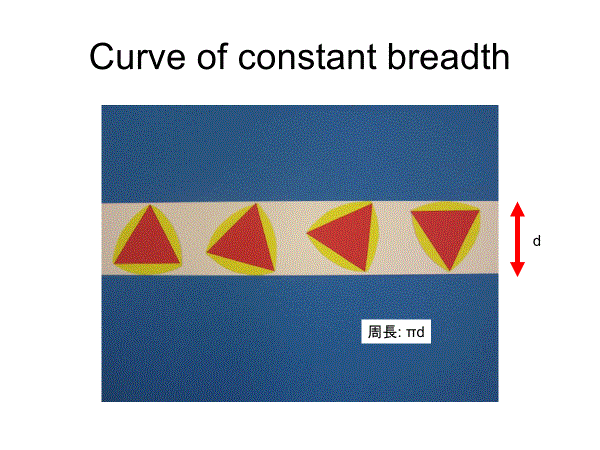
幅をdとすると、定幅曲線の周長はどれも等しいが、面積は円が最大、ルーローの三角形は最小となる

定理

1. There are infinitely many kinds of curves of constant breadth. Perimeters of curves of constant breadth (=d) are equal to πd (Barbier)

2. Among them, circle has largest area; πd^2/4 and arc triangle of Reuleaux has smallest area; (π-√3)d^2/2 (Blaschke, Lebesgue)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝