100年前の仙台（東北大学）発の数学問題をとりあげたい

[1]藤原松三郎の問題

　　正三角形に内接しながら回転することができる円以外の図形は何か（東北大学理科報告、１９１５年）

[2]掛谷宗一の問題

　　長さが1である線分を1回転させるのに必要な最小面積の図形は何か（東北数学雑誌、１９１７年）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

掛谷の問題のほうが有名ではあると思われるが、前者は後者の原型になった問題である

古典的とはいえど、新しい応用や未解決の問題を含んでいる・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

掛谷の問題から始めたい。

デルトイドでは接線の長さは常に１であり、その中心の軌跡は円である

したがって、多くの数学者はデルトイドが解であり、最小面積はπ/8であると予想した。

ところが、その予想に反して、１９２７年、ベシコヴィッチが面積を限りなく０に近づけることのできる図形を構成した。

驚愕の結果であった。この直観に反する結果はベシコヴィッチ・ショックと呼んでよいものであろう。

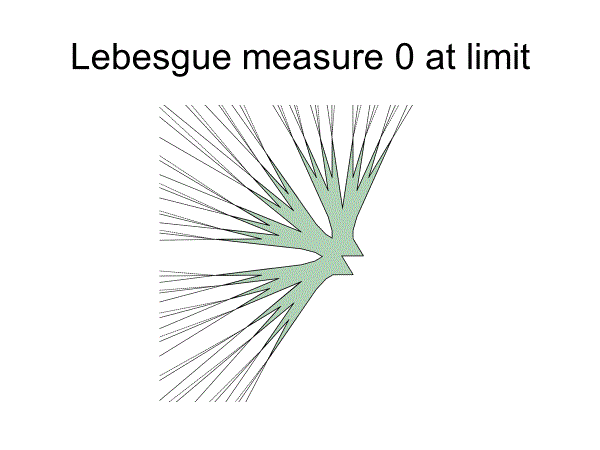
定理(Besicovitch,1927)

For given ε>0, there exists Kakeya set of area less than ε.

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝