■18世紀における微積分(その64)
回転円が固定円に接して滑ることなく転がっていくとき,回転円の周上の点の軌跡を考えます.回転円が固定円に外接するとき,その軌跡をエピサイクロイド,内接するとき,ハイポサイクロイドと呼びます.
アステロイド: x^2/3 +y^2/3 =a^2/3 は固定円の半径が回転円の半径の4倍になっているハイポサイクロイドです
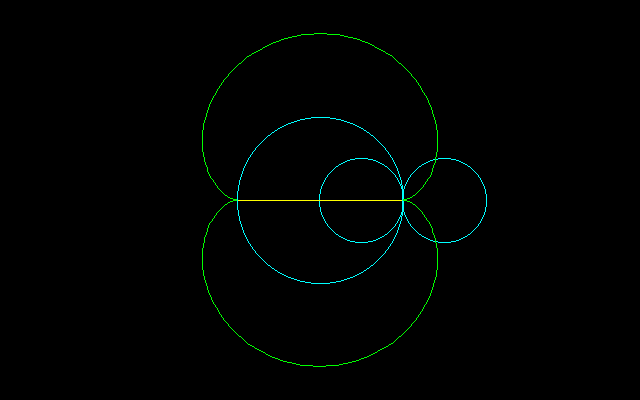
固定円と回転円の半径が等しいエピサイクロイドは心臓型曲線(カージオイド)を描きます。
エピサイクロイド(カージオイド、ネフロイドなど)、ハイポサイクロド(デルトイド、アステロイドなど)は、サイクロイドとは異なり代数曲線です。
ここでは鉢形曲線の面積を求めてみます
===================================
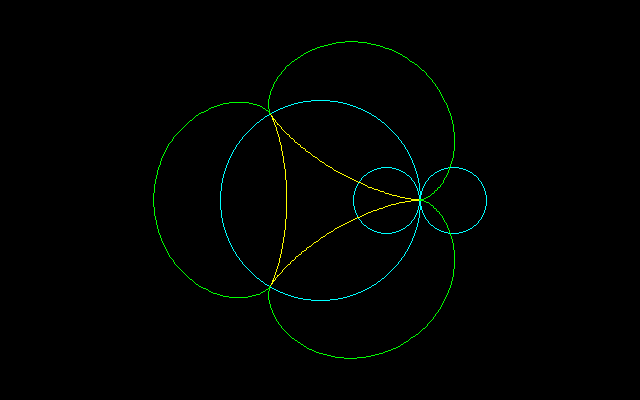
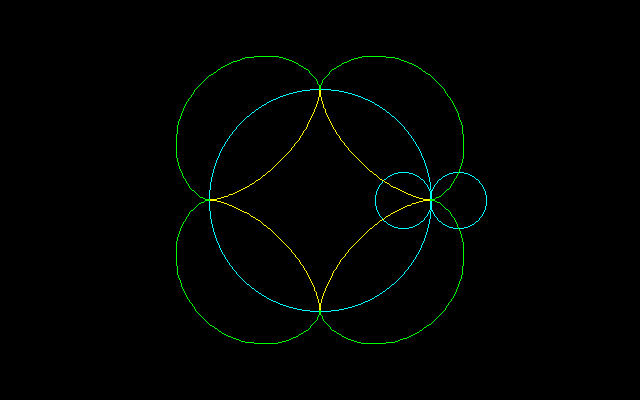
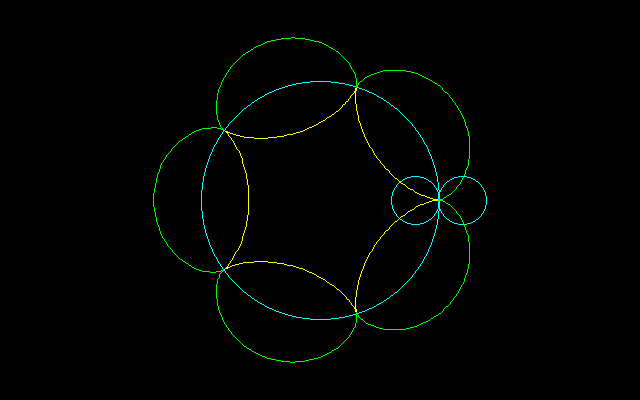
回転円の半径が1のとき、n尖点エピサイクロイドとn尖点ハイポサイクロイドの間の鉢形曲線の周長と面積は
L={(8n+1)+(8n-1)}/n=16
S={(n+1)(n+2)-(n-1)(n-2)}/n・π=6π
サイクロイド (L=8, S=3π)
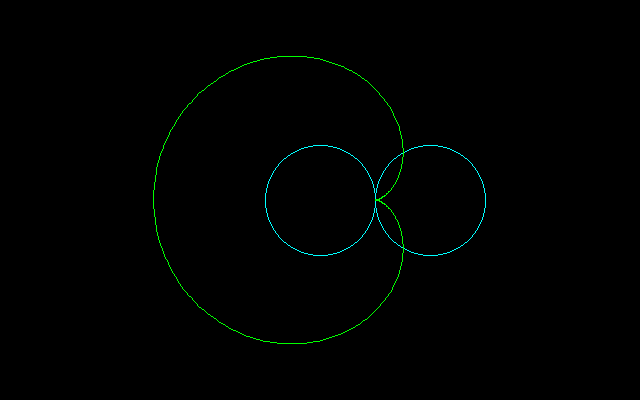
カージオイド (L=16, S=6π)
===================================







