サイクロイドは自転車の車輪に固定された点の軌跡である。

古代ギリシャの人々は固定円上の回転円を使って惑星の軌道を説明した。しかし、円周の代わりに直線上を移動させることはギリシャ人から関心を示されることはなかった 。

サイクロイドは長い間忘れ去られた曲線であったが、円と直線のごく自然な組み合わせからなり、 (直線や円の次に)最も自然な曲線として、ガリレオによってサイクロイドという名前が与えられた (1599年)。

[Q]サイクロイド弧が囲む面積は?

[Q]サイクロイド弧長は?

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

17世紀初め、サイクロイドが囲む面積の計算は当時の偉大な数学者たちの関心の的であり、中心的な問題でもあった。

[A]回転円の3倍

[A]弧長は回転円に外接する 正方形の周に等しい

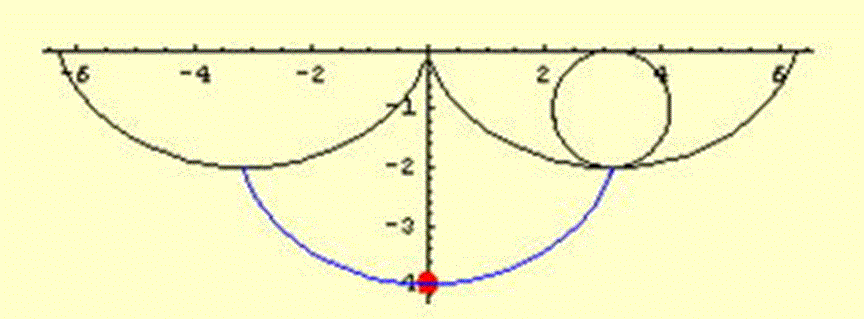
サイクロイドのインボリュートは合同なサイクロイドである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

サイクロイドはホイヘンスによって振子時計の設計に使われ、そしてパスカルの積分法の研究に貢献した。

ホイヘンスはサイクロイドが等時曲線（所要時間が質点の位置に関係なく一定である曲線）であることを発見しました．逆に，等時性が成り立つ曲線はサイクロイドに限ることが知られています．

等時性をもつ振子を作るには振幅角が大きいとき振子の長さを短くして，錘の軌跡がサイクロイドを描くようにすればよいのですが，ホイヘンスは等時性からのずれを補正するためにサイクロイドの縮閉線を利用しました．サイクロイドの縮閉線にはもとのサイクロイドと合同なサイクロイドになるという性質があるからです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝