Ｕ嬢への返歌として，このシリーズの主役たちについてまとめておきたい．

　　大円（半径Ｒ），小円（半径ｒ），弦（長さＬ）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

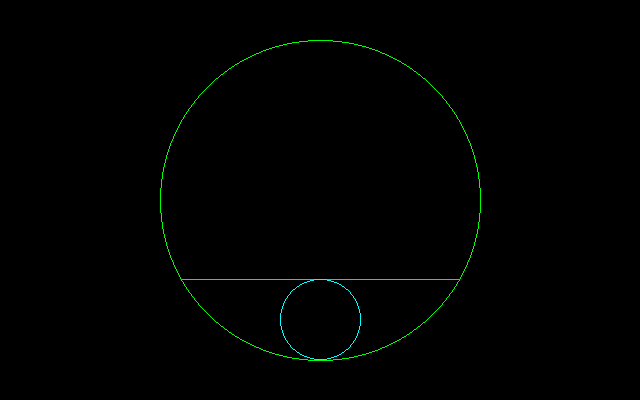
［Ｑ１］Ｌとｒが所与のとき，Ｒを求めよ．

［Ａ１］ピタゴラスの定理より，

　　Ｒ^2＝（Ｌ／２）2＋（Ｒ−２ｒ）^2

　　４Ｒｒ＝Ｌ^2／４＋４ｒ^2

　　Ｒ＝Ｌ^2／１６ｒ＋ｒ

［Ｑ２］Ｑ１の図形を縦軸を中心として回転させたときに，弦より上にできる回転体の体積は？

［Ａ２］省略

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

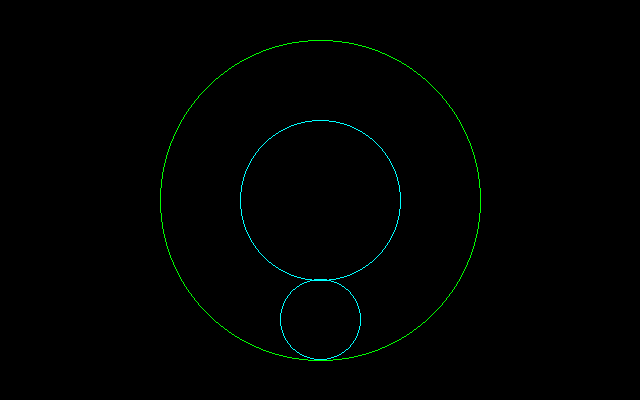
［Ｑ３］蛇の目模様において，同心円の間にある面積Ｓと小円の半径ｒが所与のとき，中円の半径Ｍを求めよ．

［Ａ２］π（Ｒ^2−Ｍ^2）＝Ｓ，Ｒ−Ｍ＝２ｒより

　　π（（Ｍ＋２ｒ）^2−Ｍ^2）＝Ｓ→π（４Ｍｒ＋４ｒ^2）＝Ｓ

あるいは

　　Ｒ＋Ｍ＝Ｓ／π（Ｒ−Ｍ）＝Ｓ／２πｒ

　　Ｍ＝Ｓ／４πｒ−ｒ

［Ｑ４］同心球の間にある体積Ｖと小球の半径ｒが所与のとき，中球の半径Ｍを求めよ．

［Ａ４］４π／３（Ｒ^3−Ｍ^3）＝Ｖ，Ｒ−Ｍ＝２ｒより

　　４π／３（（Ｍ＋２ｒ）^3−Ｍ^3）＝４π／３（６Ｍ^2ｒ＋１２Ｍｒ^2＋８ｒ^3）＝Ｖ

　Ｍに関する２次方程式

　　６Ｍ^2ｒ＋１２Ｍｒ^2＋８ｒ^3＝３Ｖ／４π

を解くことになる．以下，省略．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝