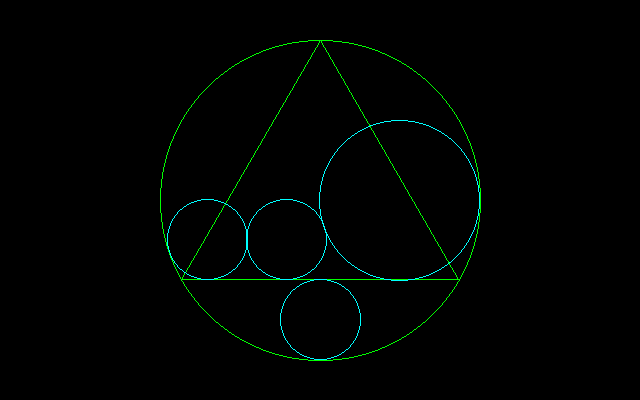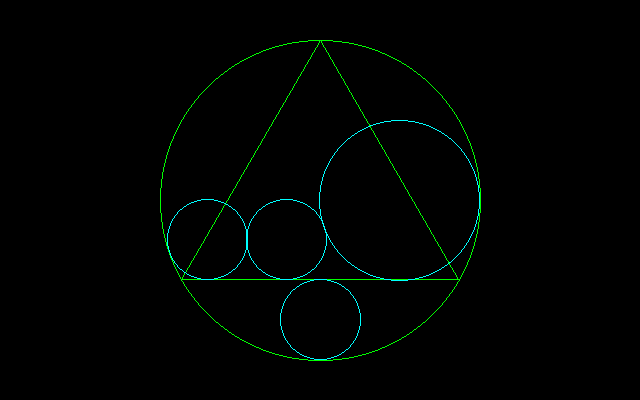和算には○△□が頻繁に登場する．図形の問題では座標を設定して，どうしても計算したくなるものであるが，

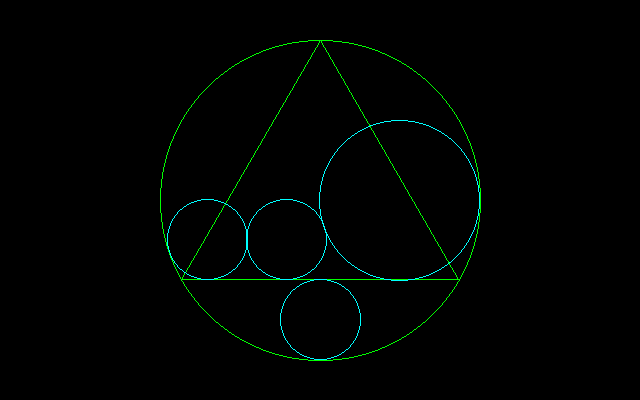
　　［Ｑ］中円の半径は？

のようにほとんど計算しなくてもよい問題もあるようだ．

　外接円の半径をＲ，内接円の半径をｒとすると，正三角形ではＲ＝２ｒ，正方形ではＲ＝√２ｒ，正ｎ角形では

　　Ｒ＝ｒｓｅｃ（π／ｎ）

また，星形ｍ／ｎ角形では

　　Ｒ＝ｒｓｅｃ（ｍπ／ｎ）

となる．

　したがって，この問題に対する一般的な解答を与えると

［１］外接円：Ｒ

［２］内接円：Ｒｃｏｓ（π／ｎ）

［３］［１］［２］に接する円：（Ｒ−Ｒｃｏｓ（π／ｎ））／２

［１］／［３］比：２／（１−ｃｏｓ（π／ｎ））

［２］／［３］比：２ｃｏｓ（π／ｎ）／（１−ｃｏｓ（π／ｎ））

　ｎ＝３のとき，［１］／［３］比＝４，［２］／［３］比＝２

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　星形ｍ／ｎ角形では

［１］外接円：Ｒ

［２］内接円：Ｒｃｏｓ（ｍπ／ｎ）

［３］［１］［２］に接する円：（Ｒ−Ｒｃｏｓ（ｍπ／ｎ））／２

［１］／［３］比：２／（１−ｃｏｓ（ｍπ／ｎ））

［２］／［３］比：２ｃｏｓ（ｍπ／ｎ）／（１−ｃｏｓ（ｍπ／ｎ））

となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝